A bobbin rolls without slipping over a horizontal surface so that the velocity v of the end of the thread (point A) is directed along the horizontal . A board hinged at point B leans against the bobbin (Fig.) The inner and outer radii of the bobbin are r and R respectively. Determine the angular velocity ω of teh board as a function of an angle α.

Step by step video & image solution for A bobbin rolls without slipping over a horizontal surface so that the velocity v of the end of the thread (point A) is directed along the horizontal . A board hinged at point B leans against the bobbin (Fig.) The inner and outer radii of the bobbin are r and R respectively. Determine the angular velocity omega of teh board as a function of an angle alpha. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.
 View Solution
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View Solution
Knowledge Check
- Question 1 - Select One
A ring of radius R rolls without slipping on a rough horizontal surface with a constant velocity. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
 .ARB2 RC4 RDnone of these
.ARB2 RC4 RDnone of these - Question 2 - Select One
A uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
 Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0
Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0 - Question 3 - Select One
A bobbin is pushed along on a rough stationary horizontal surface as shown in the figure. The board is kept horizontal and there is no slipping at any contact points. The distance movedby the board when distance moved by the axis of the bobbin is l is
 .Al(1+r2R)Bl(2+r2R)Cl(1+rR)Dl(1+2rR)
.Al(1+r2R)Bl(2+r2R)Cl(1+rR)Dl(1+2rR)
A circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionA cylinder rolls without slipping over a horizontal plane. The radius of the cylinder is equal to r. Find the curvature radii of trajectories traced out by the points A and B(see figure)
 View Solution
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
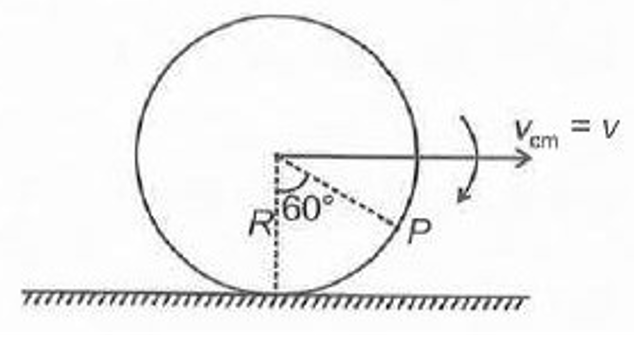 View Solution
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution

