Three forces 20√2N,20√2N and 40N are acting along X,Y and Z−axes respectively on a 5√2kg mass at rest at the origin. The magnitude of its displacement after 5s is .
50m
25m
60m
100m
The correct Answer is:D
To solve the problem step by step, we will follow these steps:
Step 1: Identify the forces acting on the mass
The forces acting on the mass are:
- Fx=20√2N along the X-axis
- Fy=20√2N along the Y-axis
- Fz=40N along the Z-axis
Step 2: Calculate the resultant force in the XY-plane
Since the forces along the X and Y axes are perpendicular, we can calculate the resultant force Fxy using the Pythagorean theorem:
Fxy=√F2x+F2y=√(20√2)2+(20√2)2
Calculating this:
Fxy=√(400⋅2)+(400⋅2)=√800+800=√1600=40N
Step 3: Calculate the net resultant force in 3D
Now, we need to find the resultant force Fnet considering the force along the Z-axis:
Fnet=√F2xy+F2z=√(40)2+(40)2
Calculating this:
Fnet=√1600+1600=√3200=40√2N
Step 4: Calculate the acceleration
Using Newton's second law, F=ma, we can find the acceleration a:
a=Fnetm=40√25√2=405=8m/s2
Step 5: Calculate the displacement after 5 seconds
Since the mass is initially at rest, we can use the equation of motion:
s=ut+12at2
Where:
- u=0 (initial velocity)
- a=8m/s2
- t=5s
Substituting the values:
s=0⋅5+12⋅8⋅(5)2=0+12⋅8⋅25=4⋅25=100m
Final Answer
The magnitude of the displacement after 5 seconds is 100m.
---
The forces acting on the mass are:
- Fx=20√2N along the X-axis
- Fy=20√2N along the Y-axis
- Fz=40N along the Z-axis
Since the forces along the X and Y axes are perpendicular, we can calculate the resultant force Fxy using the Pythagorean theorem:
Fxy=√F2x+F2y=√(20√2)2+(20√2)2
Calculating this:
Fxy=√(400⋅2)+(400⋅2)=√800+800=√1600=40N
Now, we need to find the resultant force Fnet considering the force along the Z-axis:
Fnet=√F2xy+F2z=√(40)2+(40)2
Calculating this:
Fnet=√1600+1600=√3200=40√2N
Using Newton's second law, F=ma, we can find the acceleration a:
a=Fnetm=40√25√2=405=8m/s2
Since the mass is initially at rest, we can use the equation of motion:
s=ut+12at2
Where:
- u=0 (initial velocity)
- a=8m/s2
- t=5s
s=0⋅5+12⋅8⋅(5)2=0+12⋅8⋅25=4⋅25=100m
The magnitude of the displacement after 5 seconds is 100m.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -III31videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - NCERT BASED QUESTION33videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -I (C.W)47videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV41videos
OSCILLATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Forces of 4 N and 5 N are applied at origin along X-axis and Y-axis respectively. The resultant force will be
A√41N,tan−1(54)B√41N,tan−1(45)C−√41N,tan−1(54)D−√41N,tan−1(45) - Question 2 - Select One
Five forces 2N,√3N,5N,√3and2N respectively act at a particel P as shown in figure.
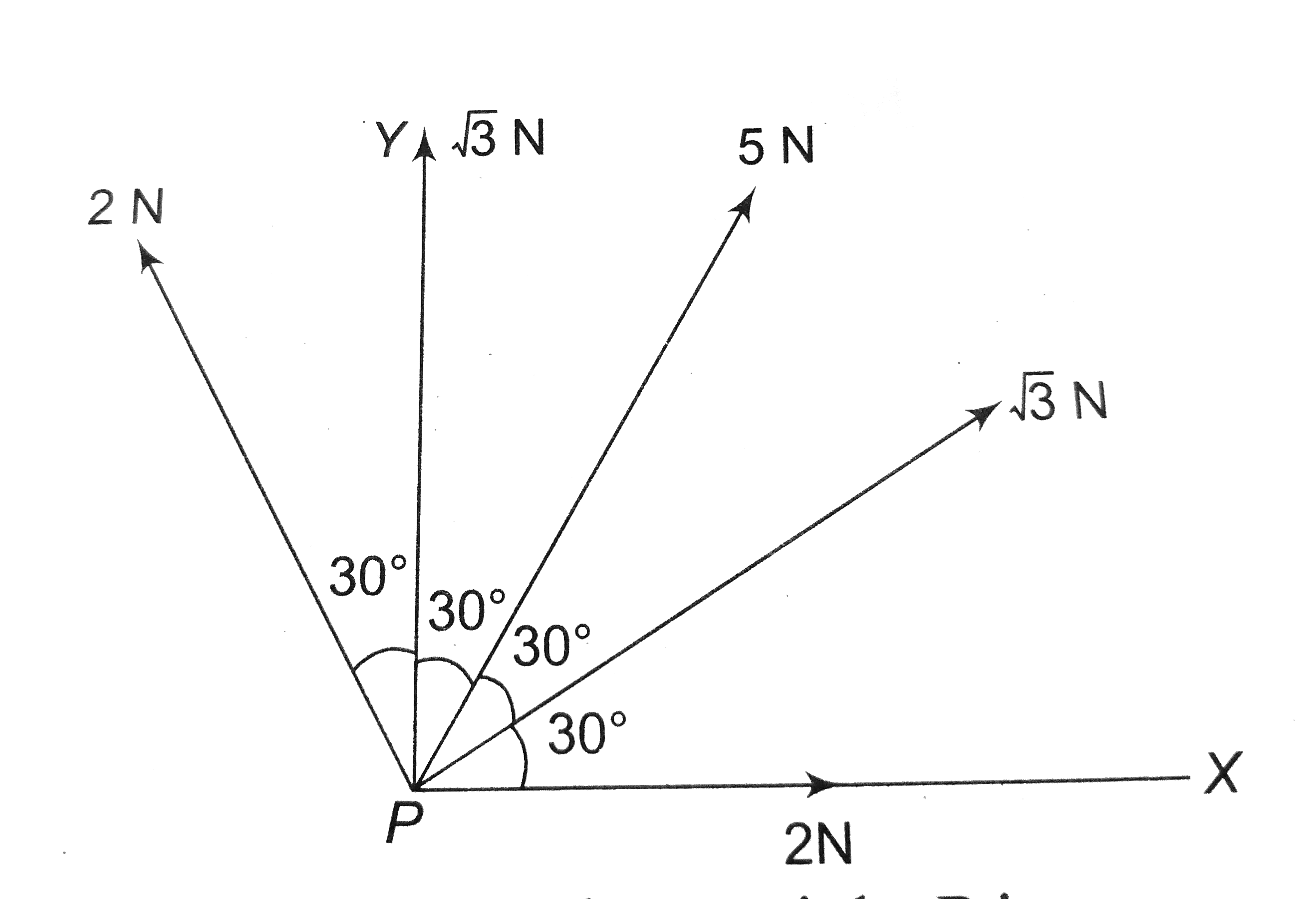
The resultant force on the particle P isA10N making angle 60∘ with X-axisB10N making angle 60∘ with Y-axisC20N along Y-axisDNone of these - Question 3 - Select One
The two forces 2√2N and xN are acting at a point their resultant is perpendicular to ˆxN and having magnitude of √6N.The angle between the two forces and magnitude of x are.
Aθ=120∘,X=√2NBθ=30∘,X=√2NCθ=150∘,X=√3NDθ=150∘,X=√2N
Forces of 5√2 and 6√2N are acting on a body of mass 1000 kg at an angle of 60∘ to each other. Find the acceleration, distance covered and the velocity of the mass after 10 s.
View SolutionForces of √2N and 6√2N are acting on a body of mass 10 kg at an angle of 60∘ to each other . Find the acceleration , distance covered and velocity of the body after 10 second , if the body is initially at rest .
View SolutionThree ant P,Q and R are pulling a grain with forces of magnitude 6N,3√3N and 3√2N as shown in the figure. Find the magnitude of resultant force (in N ) acting on the grain .
 View Solution
View SolutionForces X,Y and Z have magnitudes 10N5(√3−1)N and 5(√3+1)N, respectively. The forces Y and Z act in the same direction as shown in (figure) The resultant of X and Y and the resultant of X and Z have the same magnitudes. Find θ, the angle between X and Y.
 View Solution
View SolutionIf two forces of 5 N each are acting along X and Y axes, then the magnitude and direction of resultant is
View Solution