Question

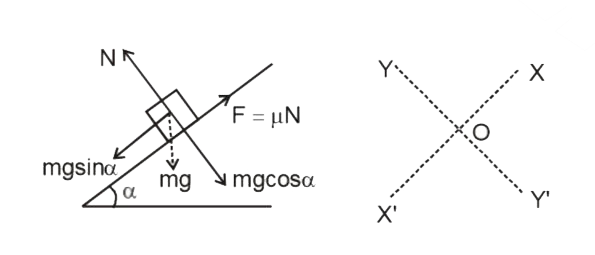
A $30kg$ box has to move up an inclined plane of slope ${30}^{\circ }$ the horizontal with a unform velocity of $5m{s}^{-1}$. If the frictional force retarding the motion is $150N$, the horizontal force required to move the box up is $(g=m{s}^{-2})$ .

Options

A. `300xx(2)/sqrt3N`
B. `300xx(sqrt3)/(2)N`
C. `300N`
D. `150N`

Answer

A

Explanation

To solve the problem of finding the horizontal force required to move a 30 kg box up an inclined plane at an angle of 30 degrees with a uniform velocity of 5 m/s, we can follow these steps:

Step 1: Identify the forces acting on the box
The forces acting on the box include:
- The weight of the box (mg), where m = 30 kg and g = 9.81 m/s².
- The component of the weight acting down the incline (mg sin θ).
- The normal force (N) acting perpendicular to the incline.
- The frictional force (F_friction) opposing the motion, which is given as 150 N.

Step 2: Calculate the weight of the box
The weight (W) of the box can be calculated as:
\( W = mg = 30 \, \text{kg} \times 9.81 \, \text{m/s}^2 = 294.3 \, \text{N} \)

Step 3: Calculate the components of the weight
The component of the weight acting down the incline (W_parallel) is given by:
\( W_{\text{parallel}} = mg \sin \theta \)
Where θ = 30 degrees:
\( W_{\text{parallel}} = 294.3 \, \text{N} \times \sin(30^\circ) = 294.3 \, \text{N} \times 0.5 = 147.15 \, \text{N} \)

The normal force (N) acting on the box is given by:
\( N = mg \cos \theta \)
\( N = 294.3 \, \text{N} \times \cos(30^\circ) = 294.3 \, \text{N} \times \frac{\sqrt{3}}{2} \approx 254.6 \, \text{N} \)

Step 4: Calculate the frictional force
The frictional force is given as 150 N.

Step 5: Set up the equation for the horizontal force
To move the box up the incline at a constant velocity, the total force acting up the incline must equal the sum of the forces acting down the incline (friction + component of weight):
\( F_{\text{horizontal}} \cos \theta = W_{\text{parallel}} + F_{\text{friction}} \)
Substituting the known values:
\( F_{\text{horizontal}} \cos(30^\circ) = 147.15 \, \text{N} + 150 \, \text{N} \)
\( F_{\text{horizontal}} \cos(30^\circ) = 297.15 \, \text{N} \)

Step 6: Solve for the horizontal force
Now, we can solve for \( F_{\text{horizontal}} \):
\( F_{\text{horizontal}} = \frac{297.15 \, \text{N}}{\cos(30^\circ)} \)
Since \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \):
\( F_{\text{horizontal}} = \frac{297.15 \, \text{N}}{\frac{\sqrt{3}}{2}} = 297.15 \, \text{N} \times \frac{2}{\sqrt{3}} \approx 342.5 \, \text{N} \)

Final Answer
Thus, the horizontal force required to move the box up the incline is approximately 342.5 N.