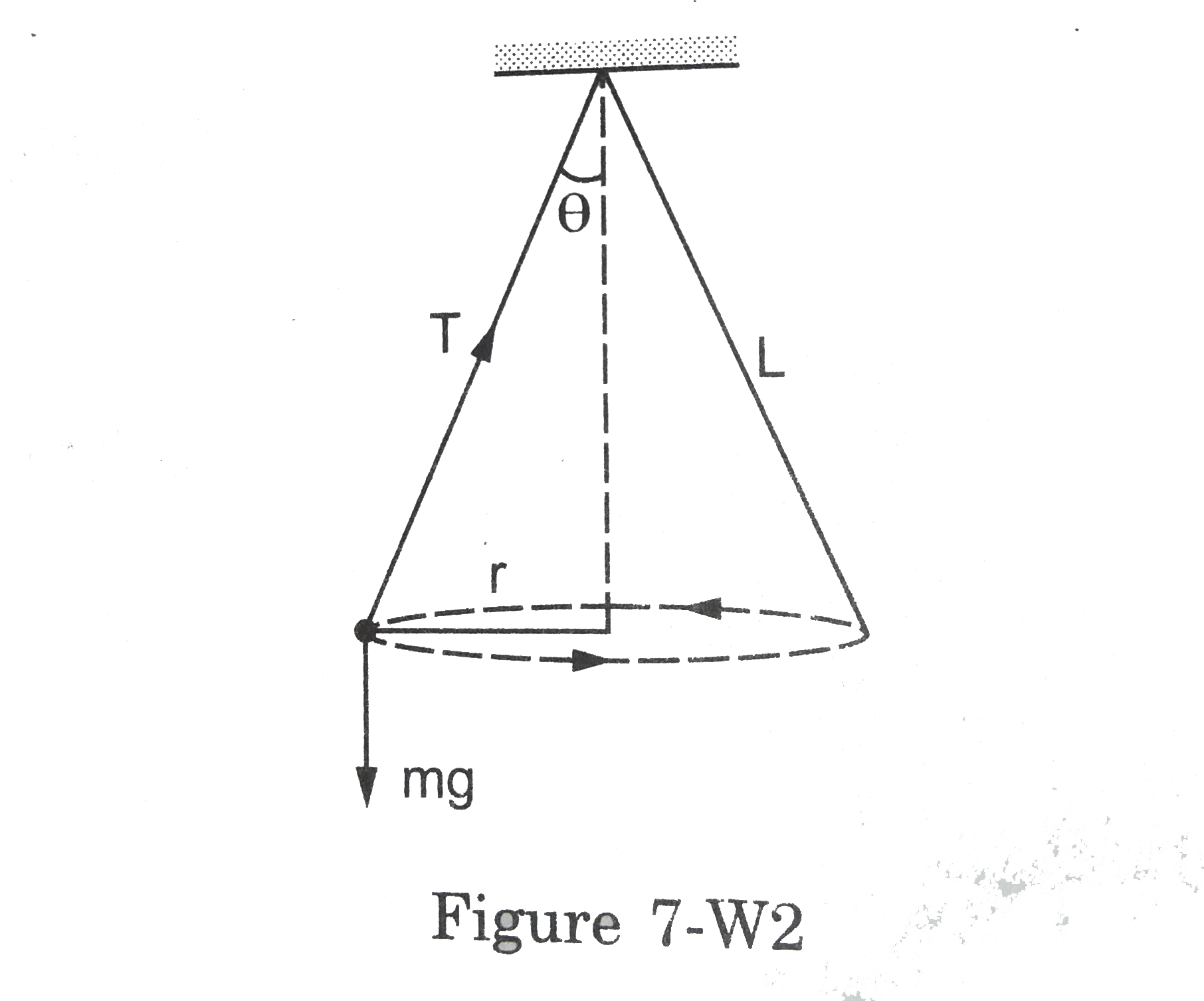
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Sch a system is called a conical pendulum.

A

$\frac{r g}{\sqrt{L^{2} - r^{2}}}$

B

$\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$

C

$\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$

D

$\frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$\frac{F}{r} = \frac{m g}{\sqrt{L^{2} - r^{2}}}$

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass ma is suspended from a ceiling thrugh a string of length $L$ . The prticle moves in a horizontal circle of radius $r$ . Find $(a)$ the speed of the prticle and $(b)$ . the tension in the string. Sch a system is called a conical pendulum
.
A $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
B $v = \frac{r^{2} \sqrt{g}}{{(L^{3} - r^{3})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
C $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L^{2}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
D $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$
Question 2 - Select One
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
A $\frac{r g}{\sqrt{L^{2} - r^{2}}}$
B $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$
C $\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
D $\frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
Question 3 - Select One
A paricle of mass $m$ is tied to a light string of length $L$ and moving in a horizontal circle of radius $r$ with speed $v$ as shown. The forces acting on the particle are

A $m g and T$
B $m g, T, \frac{m v^{2}}{r}$ directed in wards
C $m g, T, \frac{m v^{2}}{r}$ directed outewards
D $\frac{m v^{2}}{r}$ only

NARAYNA-NEWTONS LAWS OF MOTION-LEVEL -II (C.W)

Home
Ask Doubt
Profile