If a block moving up an inclined plane at 30∘ with a velocity of 5 m/s, stops after 0.5 s, then coefficient of friction will be nearly
0.5
0.6
0.9
1.1
To find the coefficient of friction (μ) for a block moving up an inclined plane at an angle of 30∘ with an initial velocity of 5m/s that stops after 0.5s, we can follow these steps:
Step 1: Calculate the Retardation (Acceleration)
The block stops after 0.5s, so we can use the equation of motion:
v=u+at
Where:
- v = final velocity = 0m/s (since it stops)
- u = initial velocity = 5m/s
- a = acceleration (which will be negative since it's retardation)
- t = time = 0.5s
Rearranging the equation to find a:
0=5+a(0.5)
a(0.5)=−5
a=−50.5=−10m/s2
Step 2: Analyze Forces on the Inclined Plane
The forces acting on the block are:
1. Gravitational force component down the incline: mgsinθ
2. Frictional force acting down the incline: f=μmgcosθ
Where:
- m = mass of the block
- g = acceleration due to gravity (approximately 10m/s2)
- θ=30∘
Step 3: Write the Equation of Motion
According to Newton's second law, the net force acting on the block can be expressed as:
mgsinθ+μmgcosθ=ma
Substituting a=−10m/s2:
mgsin30∘+μmgcos30∘=m(−10)
Step 4: Cancel Mass (m) from the Equation
We can cancel m from both sides:
gsin30∘+μgcos30∘=−10
Step 5: Substitute Values
Using g=10m/s2:
10sin30∘+μ⋅10cos30∘=−10
Calculating sin30∘=12 and cos30∘=√32:
10⋅12+μ⋅10⋅√32=−10
This simplifies to:
5+5μ√3=−10
Step 6: Solve for μ
Rearranging gives:
5μ√3=−10−5
5μ√3=−15
μ√3=−3
μ=−3√3=−√3
Since the coefficient of friction cannot be negative, we take the absolute value:
μ=1√3≈0.577
Conclusion
Thus, the coefficient of friction (μ) is approximately 0.577.
The block stops after 0.5s, so we can use the equation of motion:
- v = final velocity = 0m/s (since it stops)
- u = initial velocity = 5m/s
- a = acceleration (which will be negative since it's retardation)
- t = time = 0.5s
The forces acting on the block are:
1. Gravitational force component down the incline: mgsinθ
2. Frictional force acting down the incline: f=μmgcosθ
- m = mass of the block
- g = acceleration due to gravity (approximately 10m/s2)
- θ=30∘
According to Newton's second law, the net force acting on the block can be expressed as:
We can cancel m from both sides:
Using g=10m/s2:
Rearranging gives:
Thus, the coefficient of friction (μ) is approximately 0.577.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
70 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Block of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-

View SolutionA block starts moving up an inclined plane of inclination 30∘ with an initial velocity of v0 . It comes back to its initial position with velocity v02 . The value of the coefficient of kinetic friction between the block and the inclined plane is close to I1000 , The nearest integer to I is ____________ .
View Solution
Knowledge Check
A block starts moving up a fixed inclined plane of inclination 60∘C with a velocityof 20ms−1 and stops after 2s. The approximate value of the coefficient of friction is [g=10ms−2]
A3B3.3C0.27D0.33A block is projected upwards with a velocity of 5 m/s from the bottom of a rough inclined plane of inclination 30° with the horizontal. It stops after 0.5 s. What is the coefficient of friction ? (g=10m/s2)
A√3B1√3C√2D√5A block of mass m is kept on an inclined plane of a lift moving down with acceleration of 2m/s2 . What should be the coefficient of friction for the block to move down with constant velocity relative relative to lift?
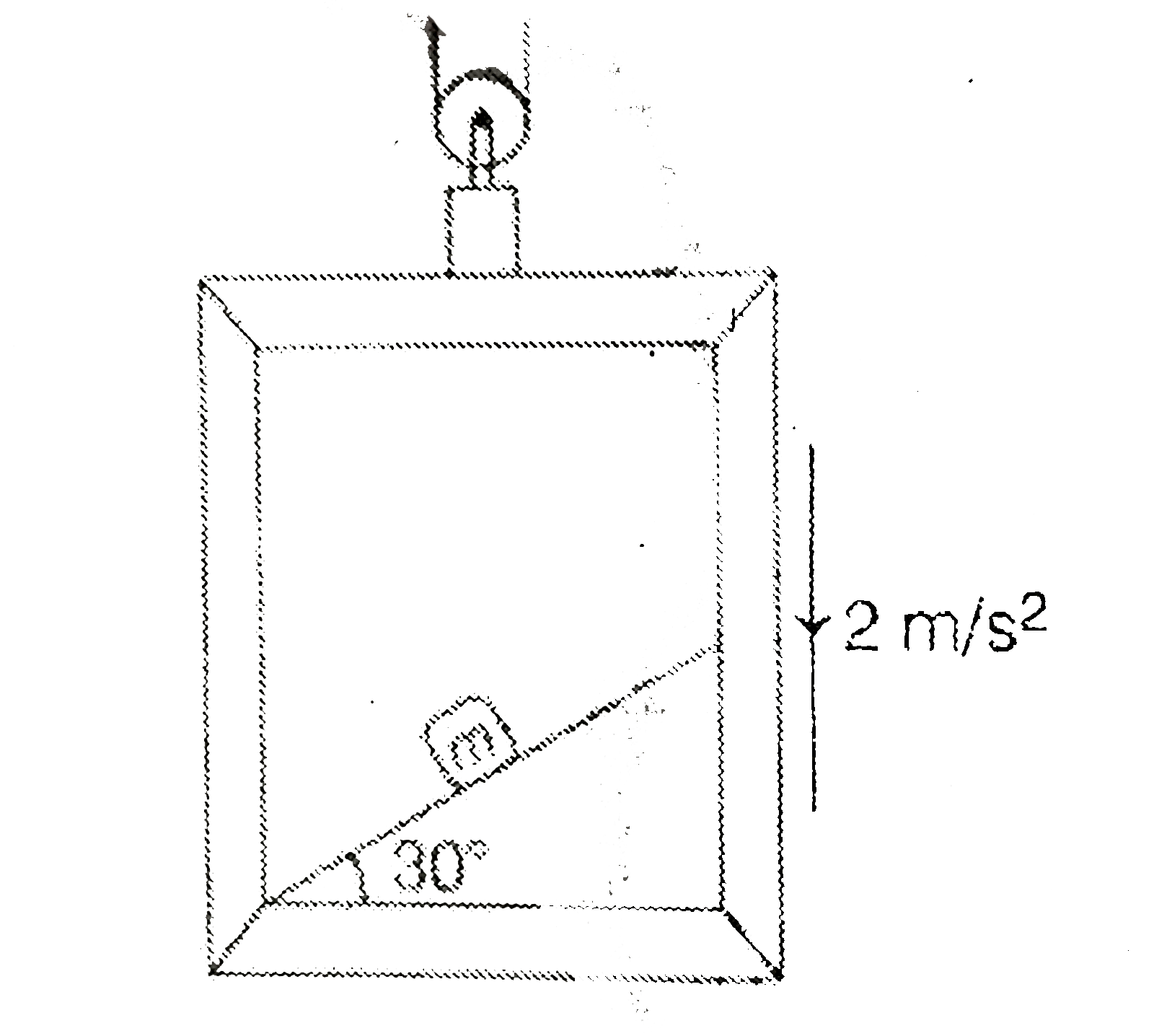 Aμ=1√3Bμ=0.4Cμ=0.8Dμ=0.5
Aμ=1√3Bμ=0.4Cμ=0.8Dμ=0.5
A 60 kg block is pushed up on inclined plane by means of a horizontal push P as shwon in the figure . The coefficients of friction between the incline and block are μs=0.6 and μk=0.4 and the ramp makes an angle of 30∘ with the horizontal .
(a) What value of P is required to move the block at a constant speed of 0.20 m/s along the incline ?
(b) If the person should stop for rest and let P = 0 , does the block slide back on the incline ?
View SolutionA block of wood of 1 kg resting on an inclined plane of angle 30∘, just starts moving down. If the coefficient of friction is 0.2, then find its velocity (in ms−1) after 5 s (take , g=10ms−2)
View SolutionA block is lying on an inclined plane which makes 60∘ with the horizontal. If coefficient of friction between block and plane is 0.25 and g=10m/s2, , then acceleration of the block when it moves along the plane will be
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View Solution
