The density of a linear rod of length L varies as where x is the distance from the left end. Locate the centre of mass.

Let the -axis be along the length of the rod and origin at one of its ends. As rod is along -axis, for all points on it and coordinates are zero.
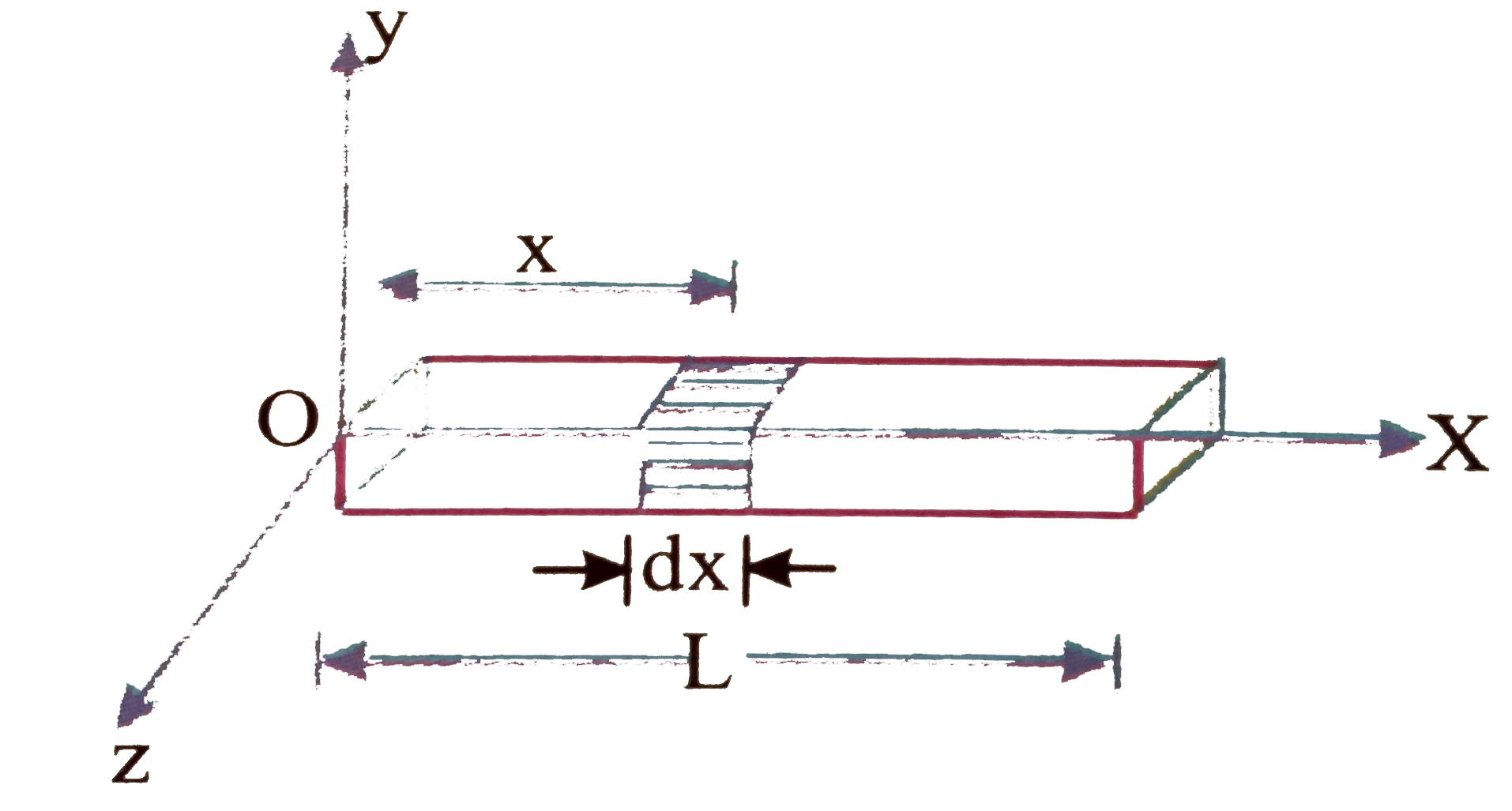
Centre of mass will be on the rod. Now consider an element of rod of length at a distance from the origin, then
Topper's Solved these Questions
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - C.U.Q.
83 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-1(C.W.)
64 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
Similar Questions
The density of a linear rod of length L varies as ρ=A+Bx where x is the distance from the left end. Locate the centre of mass.

View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View Solution
Knowledge Check
If the linear density (mass per unit length) of a rod of length 3m is proportional to x, where x, where x is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is.
A2.5 mB1 mC1.5 mD2 mA rod of length L is of non uniform cross-section. Its mass per unit length varies linearly with distance from left end. Then its centre of mass from left end is at a distance. (Take linear density at left end=0).
 AL3BL6CL2D2L3
AL3BL6CL2D2L3
If the linear density of a rod of length L varies as λ=A+Bx , find the position of its centre of mass .
View SolutionThe density of a thin rod of length l varies with the distance x from one end as ρ=ρ0x2l2. Find the position of centre of mass of rod.
View SolutionIf linear density of a rod of length 3m varies as λ=2+x, them the position of the centre of gravity of the rod is
View SolutionIf linear density of a rod of length 3m varies as λ=2+x, then the position of the centre of mass of the rod is P7m. Find the value of P.
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionThe mass per unit length of a non- uniform rod OP of length L varies as m=k(x)/(L) where k is a constant and x is the distance of any point on the rod from end 0 .The distance of the centre of mass of the rod from end 0 is
View Solution
