A conical pendulum consists of a mass M suspended from a string of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rˆi and has velocity vˆj. At time t, the angular momentum vector of the mass M about the point from which the string suspended is

MυRˆk
mυlˆk
Mυl[(√l2−R2lˆi)+Rlˆk]
−Mυl[(√l2−R2lˆi)+Rlˆk]
The correct Answer is:C
→r=Rˆi−√l2−R2ˆk
→P=Mυˆj
→L=→r×→P
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V72videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
Consider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.
 View Solution
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View Solution
Knowledge Check
- Question 1 - Select One
A conical pendulum consists of a mass M suspended from a strong sling of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rˆi and vˆj velocity. At time t the angular momentum vector of mass M about the point from which the string passes on the ceiling is
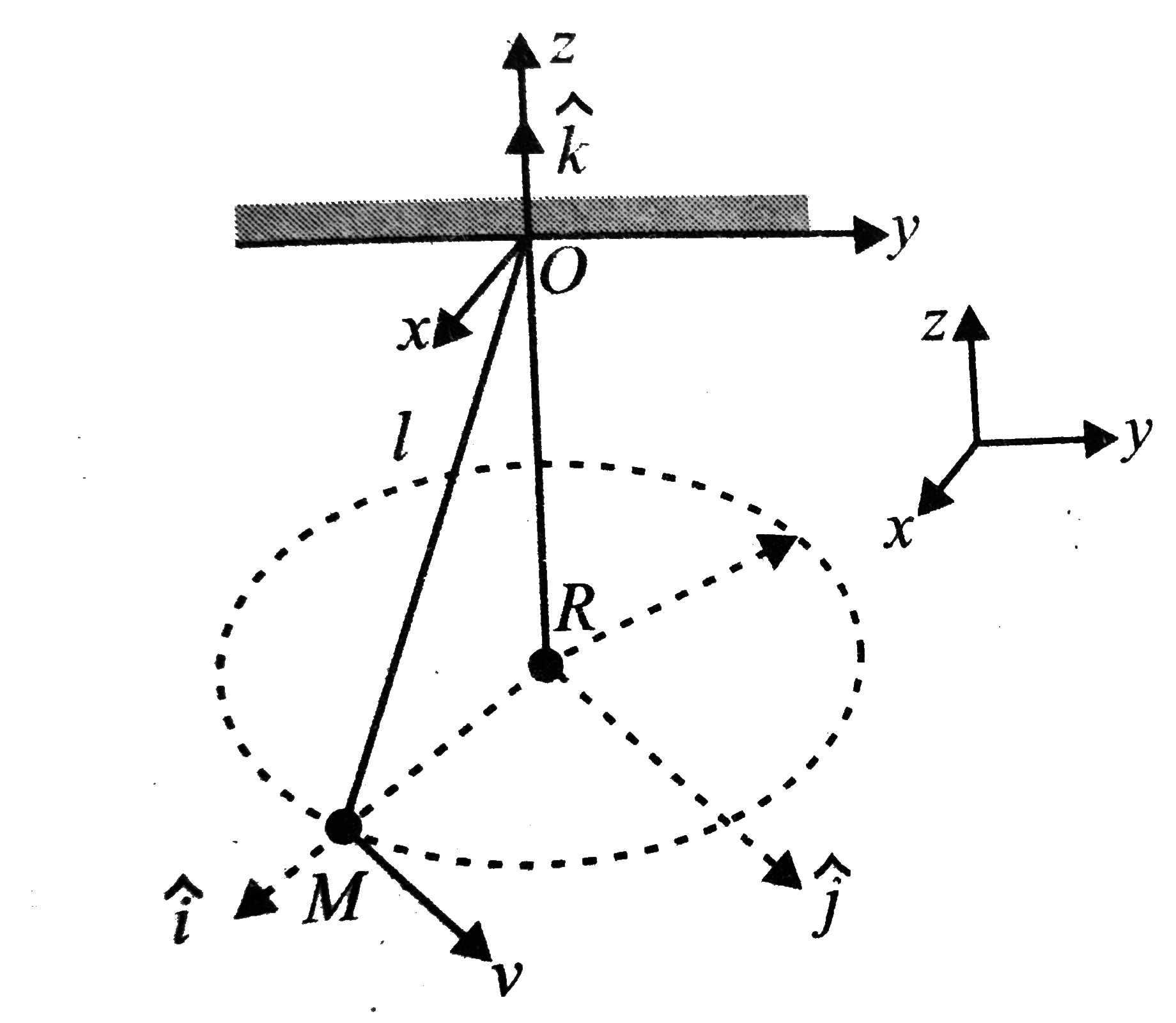 AMvRˆkBMvlˆkCMvl[√l2−R2lˆi+Rlˆk]D−Mvl[√l2−R2lˆi+Rlˆk]
AMvRˆkBMvlˆkCMvl[√l2−R2lˆi+Rlˆk]D−Mvl[√l2−R2lˆi+Rlˆk] - Question 2 - Select One
A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12 - Question 3 - Select One
A particle of mass m moves in the xy-plane with velocity of →v=vxˆi+vyˆj. When its position vector is →r=x→i+y→j, the angular momentum of the particle about the origin is.
Am(xvy+yvx)ˆkB−m(xvy+yvx)ˆkCm(yvx−xvy)ˆkDm(xvy−yvx)ˆk.
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
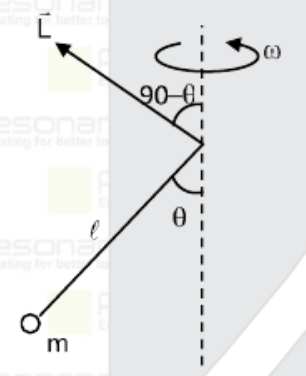 View Solution
View SolutionA stone of mass m tied to a string of length l rotates along circumference of a circle with constant speed v. The torque on the stone is
View SolutionA particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
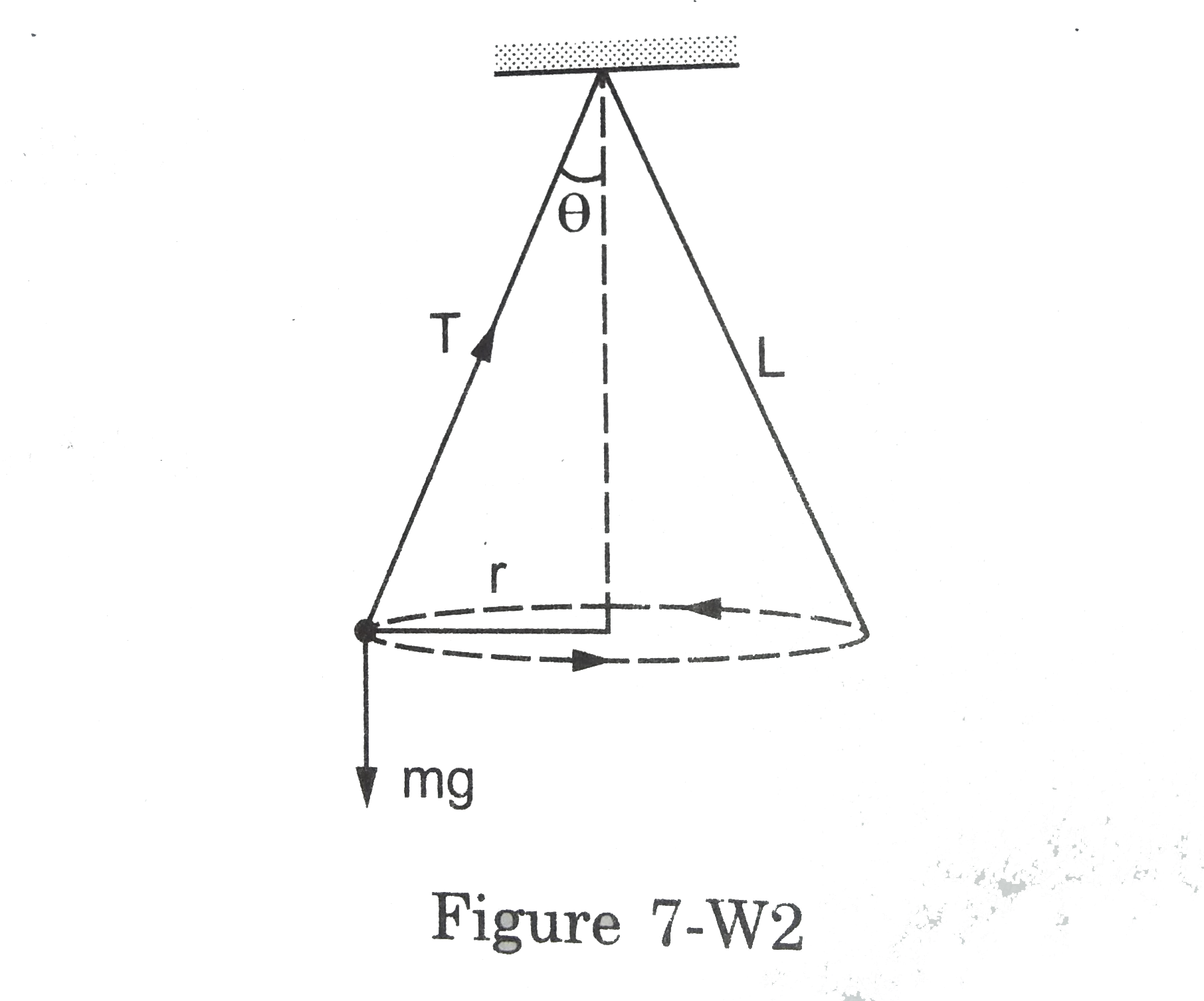
.View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 View Solution
View SolutionA stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
View Solution

