Two point masses A of mass M and B of mass of 4M are fixed at the ends

Two point masses of 0.3 kg and 0.7 kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
A0.42 in from mass of 0.3 kg
B0.70 m from mass of 0.7 kg
C0.98 m from mass of 0.3 kg
D0.98 m from mass of 0.7 kg.
Two point masses of 0.3 kg and 0.7kg are fixed at the ends of a rod of length 1.4 m and of negligible mass. The rod is set rotating about an axis perpendicular to its length with a uniform angular speed. The point on the rod through which the axis should pass in order that the work required for rotation of the rod is minimum, is located at a distance of
A0,42 m from mass of 0.3 kg
B0.70 m form mass of 0.7 kg
C0.98 m form mass of 0.3 kg
D0.98 m from mass of 0.7 kg
Point masses $m_{1} and m_{2}$ are placed at the opposite ends of a rigid rod of length $L$ , and negligible mass. The rod is to be set rotating about an axis perpendicualr to it. The position of point $P$ on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity $ω_{0}$ is minimum, is given by :

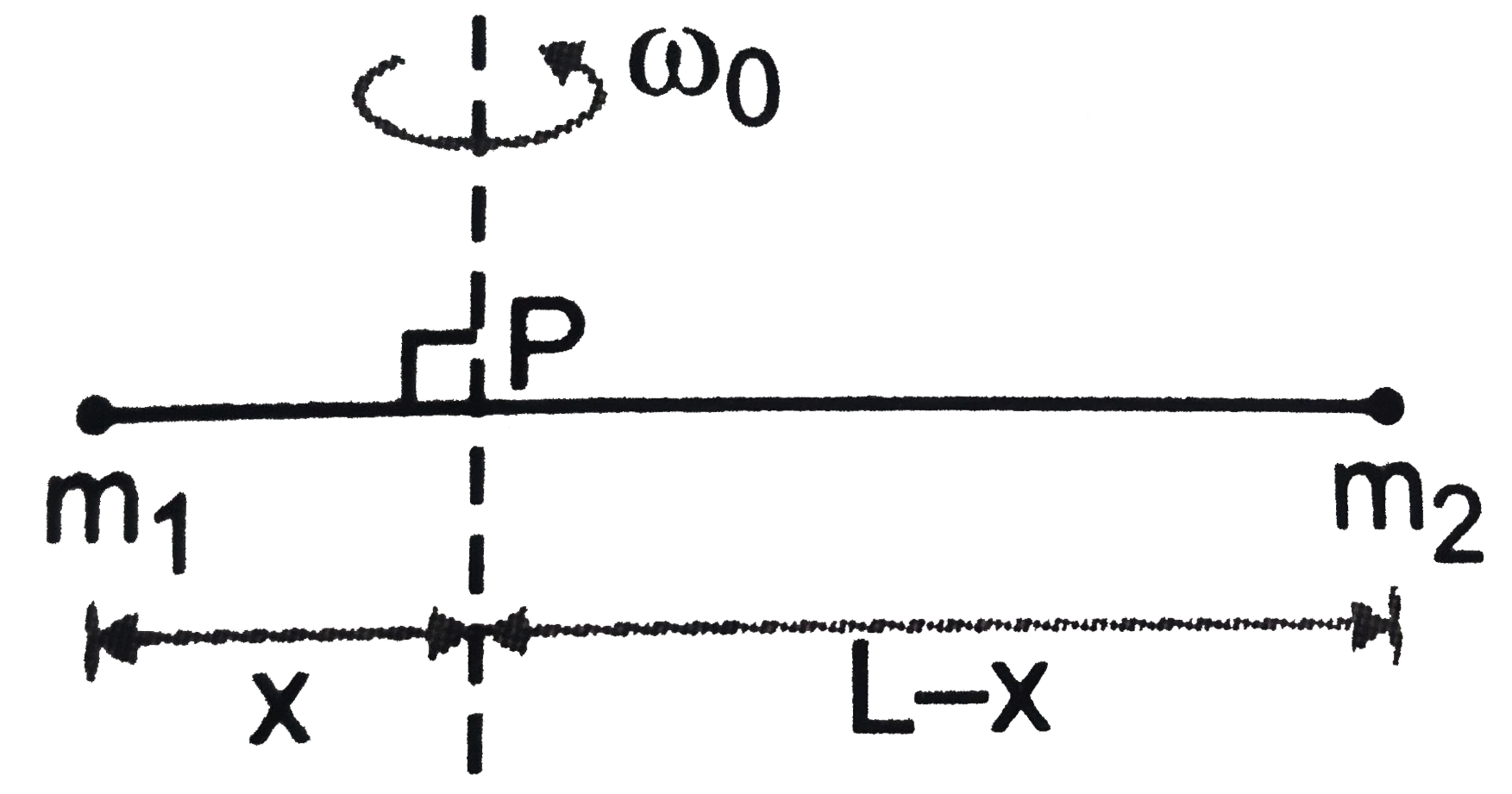A $x = \frac{m_{2} L}{m_{1} + m_{2}}$
B $x = \frac{m_{1} L}{m_{1} + m_{2}}$
C $x = \frac{m_{1}}{m_{2}} L$
D $x = \frac{m_{2}}{m_{1}} L$

The correct Answer is:C