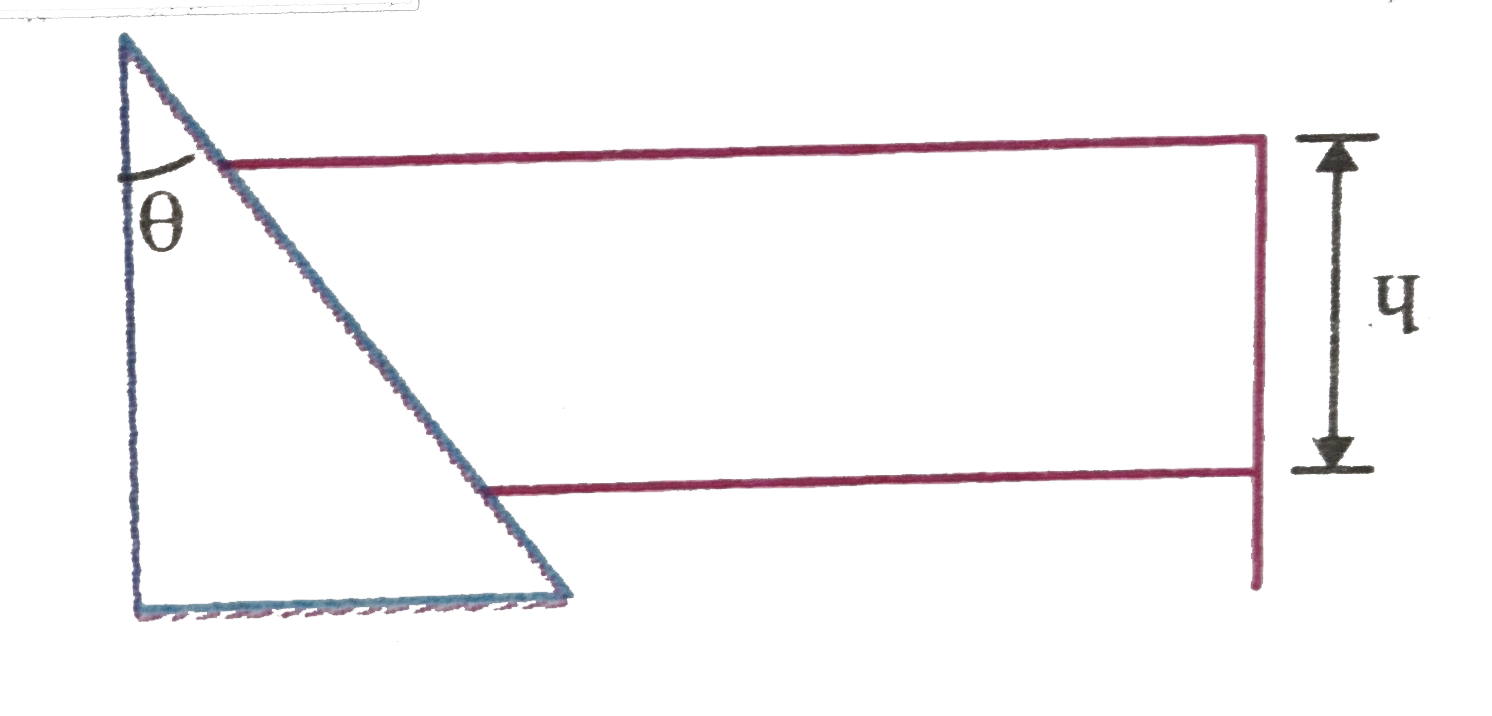
A silt is cut at the bottom, along the right bottom edge of a rectangular tank. The slit is closed by a wooden wedge of mass m and apex angle θ as shown in figure. The vertical plane surface of the wedge is in contact with the right vertical wall of the container. coefficient of static friction between these two surfaces is μ. To what maximum height can water be filled in the tank without leakage from the slit ? The width of tank is b and density of water is ρ.
√2mρb(tanθ−μ)
√4mρb(tanθ−μ)
√2mρb(sinθ−μcosθ)
√2mcosθρb(tanθ−μcosθ)
The correct Answer is:A
mg+μN=Fpressure
⇒mg+μ[ρg.h2(bh)]=ρg[12×htanθ×h]
⇒mg+μρgh2b2=ρgh2tanθ2
⇒m=bh2ρ2[tanθ−μ]∵h=√2m(tanθ−μ)bρ
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - integer Type Questions25videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 1 (H.W)55videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Paragraph Type Questions5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q13videos
MATHEMATICAL REVIEW & PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
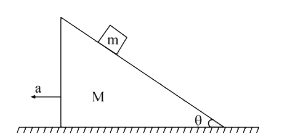 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ - Question 2 - Select One
If the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is
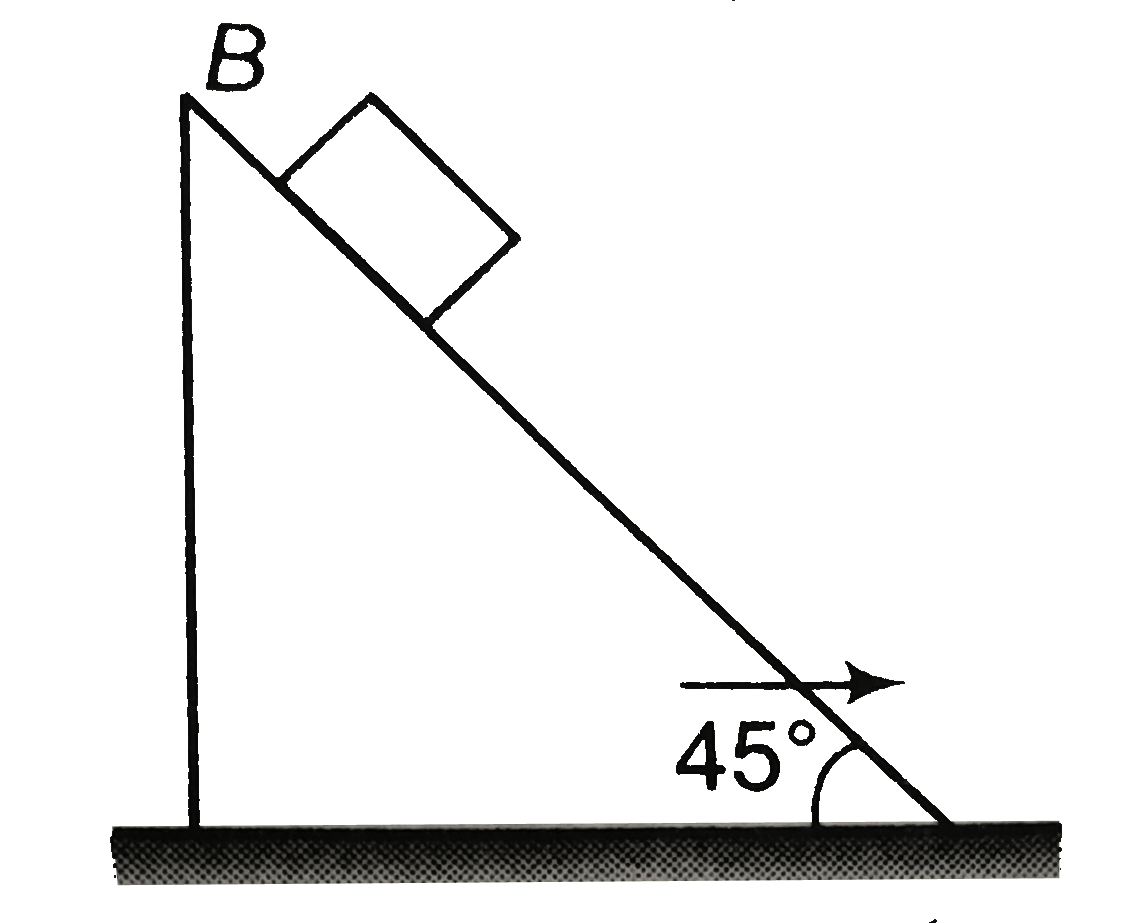 AμgBg(1+μ1−μ)Cg(1−μ1+μ)Dgμ
AμgBg(1+μ1−μ)Cg(1−μ1+μ)Dgμ - Question 3 - Select One
A mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
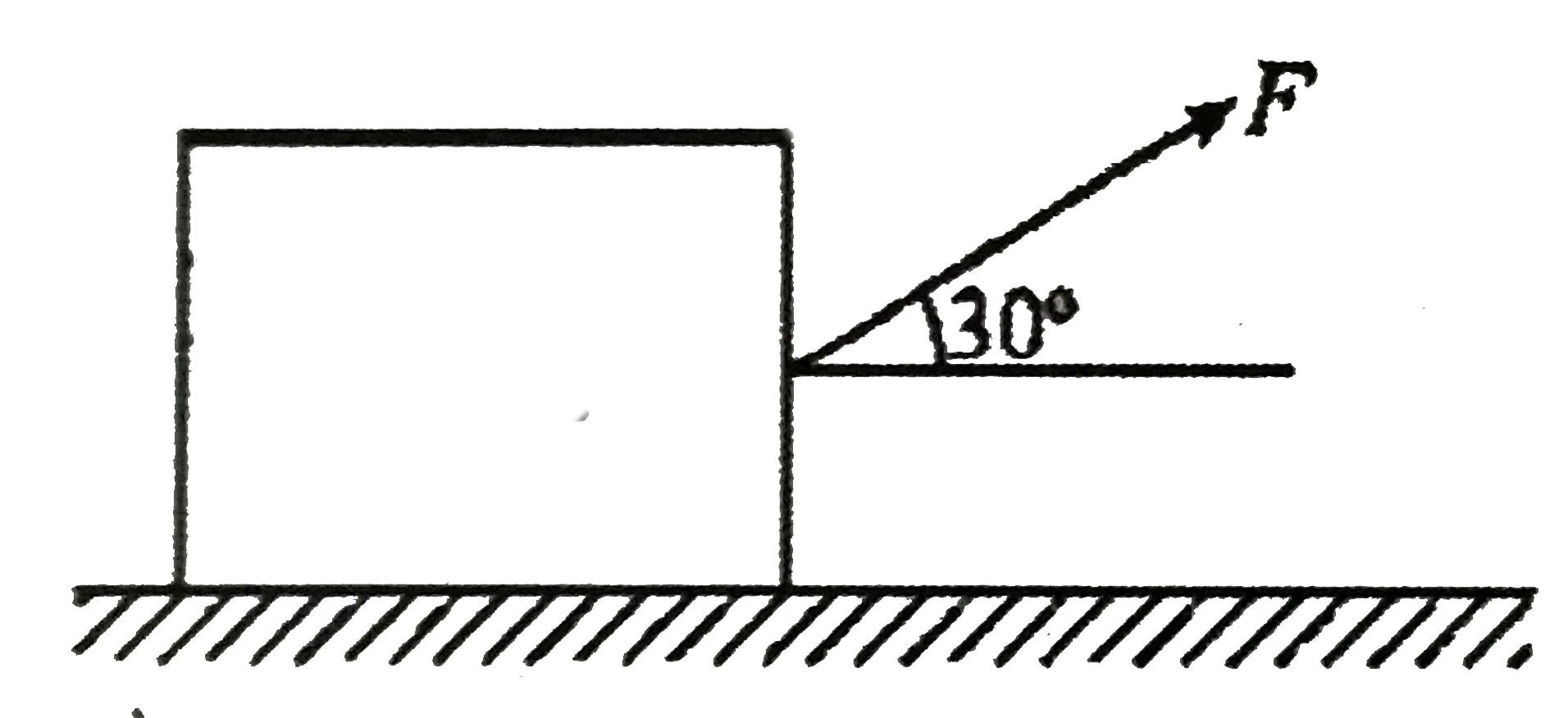 AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
The coefficient of friction between the wedge and the table is μ, the friction between the rod and the wedge being negligible.
View SolutionFind the accelerations of rod A and wedge B in the arrangement shown in figure if the ratio of the mass of the wedge to that of the rod equals η, and the friction between all contact surfaces is negligible.
 View Solution
View SolutionA block of mass m is initially lying on a wedge of mass M with an angle of inclination θ as shown in figure. Calculate the displacement of the wedge when the block is released and reaches to the bottom of the wedge.
 View Solution
View SolutionA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
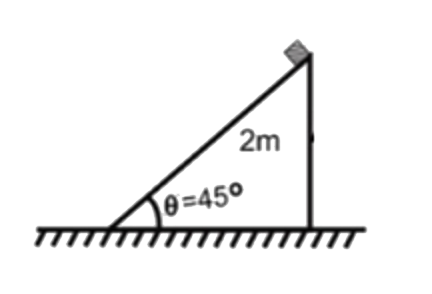 View Solution
View SolutionA wedge of mass 2m and a cube of mass m are shown in figure. Between cube and wedge, there is no friction. The minimum coefficient of friction between wedge and ground so that wedge does not move is
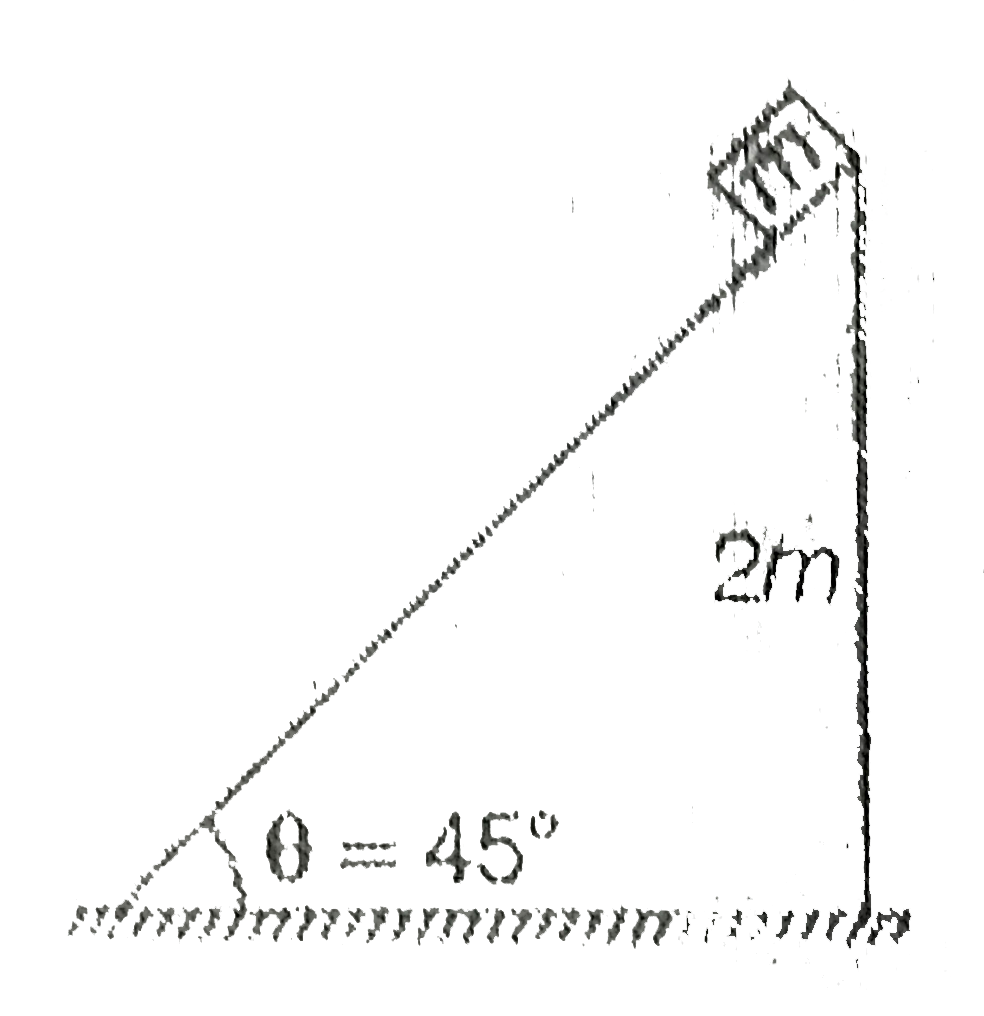 View Solution
View Solution

