
As shown in Fig. AB is rod of length 30 cm and area of cross section 1.0cm2 and thermal conductivity 336 SI units. The ends A and B are maintained at temperatures 20∘C and 40∘C, respectively .A point C of this rod is connected to a box D, containing ice at 0∘C through a highly conducting wire of negligible heat capacity. The rate at which ice melts in the box is (assume latent heat of fusion for ice Lf=80cal/g)
84mg/s
84g/s
20mg/s
40mg/s
The correct Answer is:D
dθdt=dmdtLf=(4−02)×KA+(20−01)KA
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-I(H.W)
19 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-II(C.W)
27 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - SINGLE ANSWER QUESTIONS Passage -1
1 Video
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
- UNITS AND MEASUREMENTSBOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION
23 Videos
Similar Questions
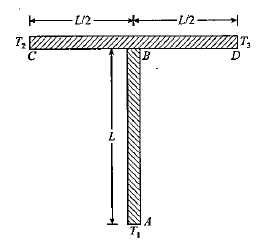
Two identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T1,T2andT3 respectively. Neglecting heat loss to the surroundings, find the temperature at B.
View SolutionFour identical rods AB, CD, CF and DE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmospere, find the temperature at B.

View Solution
Knowledge Check
All the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
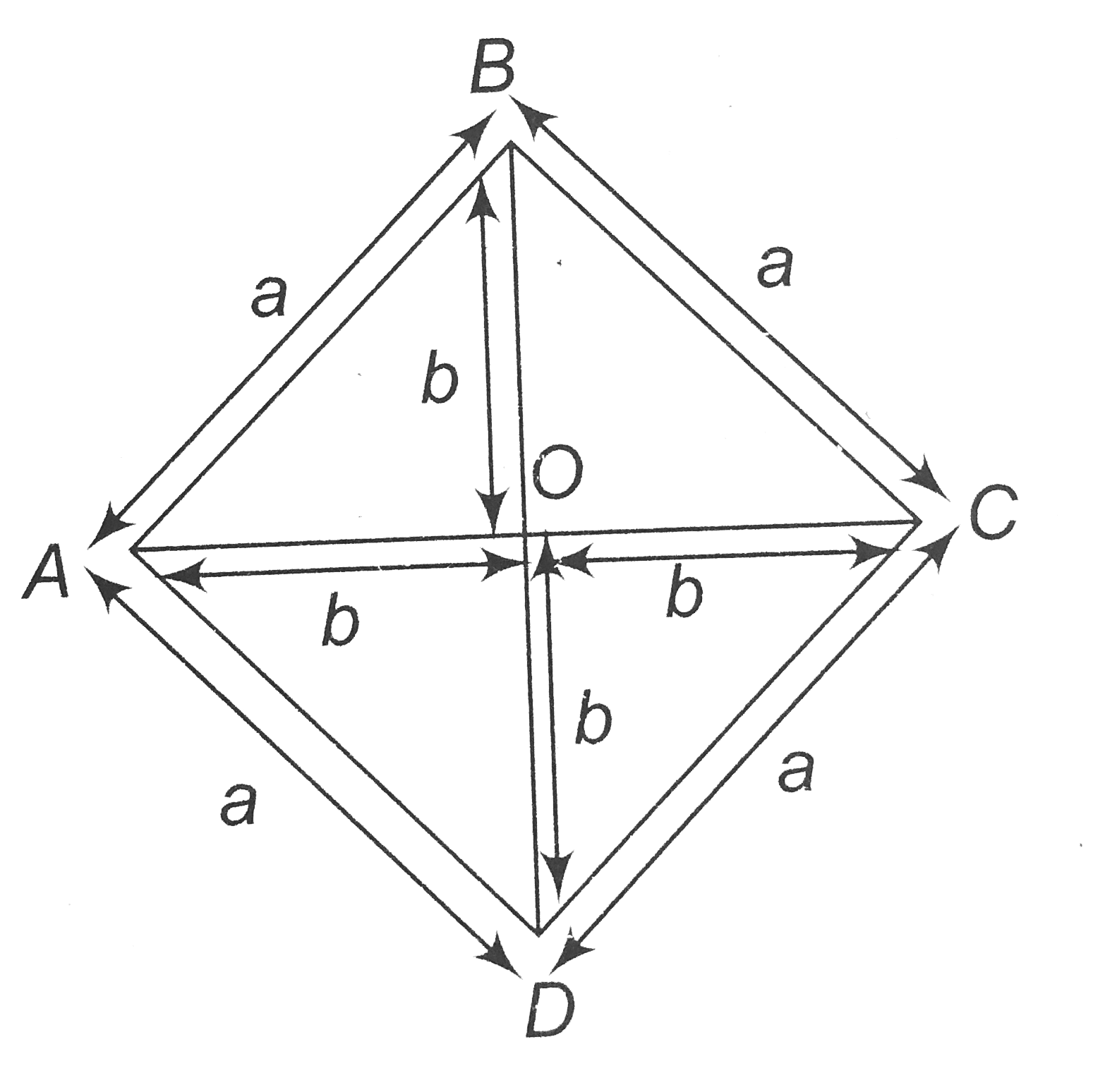 ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are sameTwo ends of a conducting rod of varying cross-section are maintained at 200∘Cand0∘C respectively. In steady state :
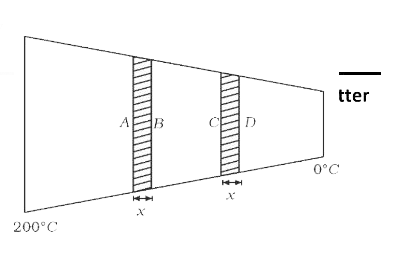 Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.Two ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:
 Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Five rods of same material and same cross-section are joined as shown. Lengths of rods ab, ad and bc are l, 2l and 3l respectively. Ends a and c are maintained at temperatures 200∘C and 0∘C respectivelly.
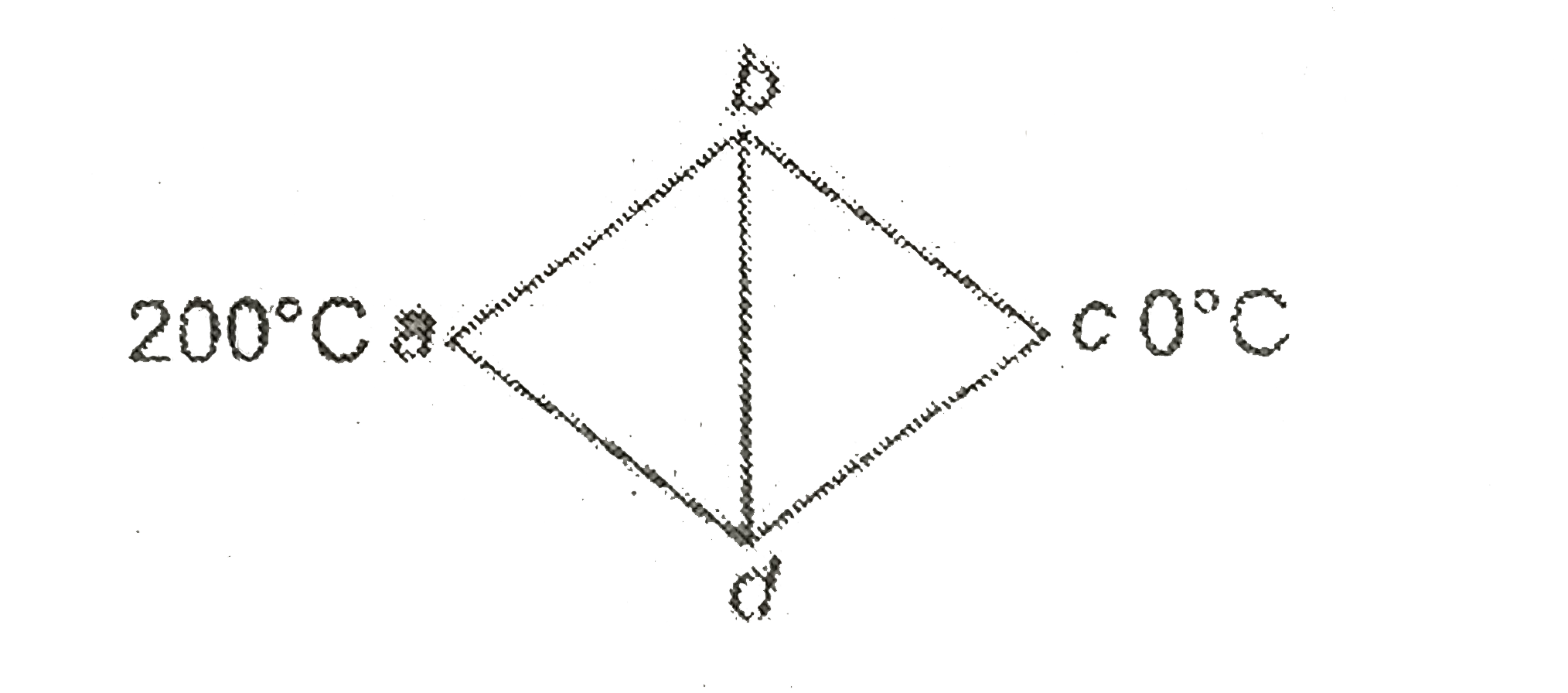
For what length x of rod dc there will be no heat flow through rod bd ?
View SolutionA heat flux of 4000 J/s is to be passed through a copper rod of length 10 cm and area of cross section 100cm2. The thermal conductivity of copper is 400W/m/∘C The two ends of this rod must be kept at a temperature difference of
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
View SolutionFive rods of same material and same cross-section are joined as shown. Lengths of rods ab, ad and bc are l, 2l and 3l respectively. Ends a and c are maintained at temperatures 200∘C and 0∘C respectivelly.
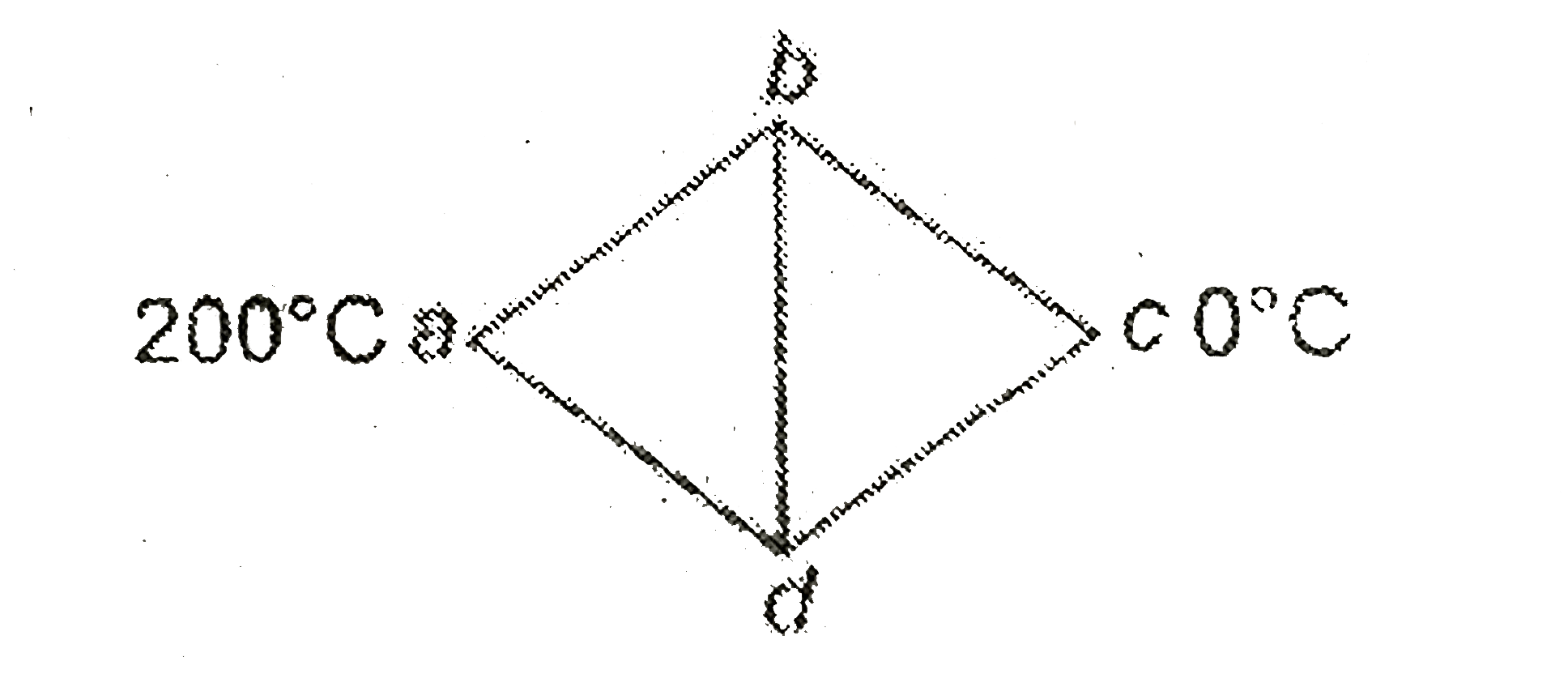
If x has the value calculated in the above question. Then temperature of junction b or d is
View SolutionOne end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
View Solution