An ideal gas expands isothermally from volume V1 to V2 and is then compressed to original volume V1 adiabatically. Initialy pressure is P1 and final pressure is P3. The total work done is W. Then
P3>P1,W>0
P3<P1,W<0
P3>P1,W<0
P3=P1,W=0
The correct Answer is:C
The slope of adiabatic process, at a given state (P,V,T) is greater than the slope of isothermal and BC is adiabatic Workdone in a process is given by area under the curve and V-axis.
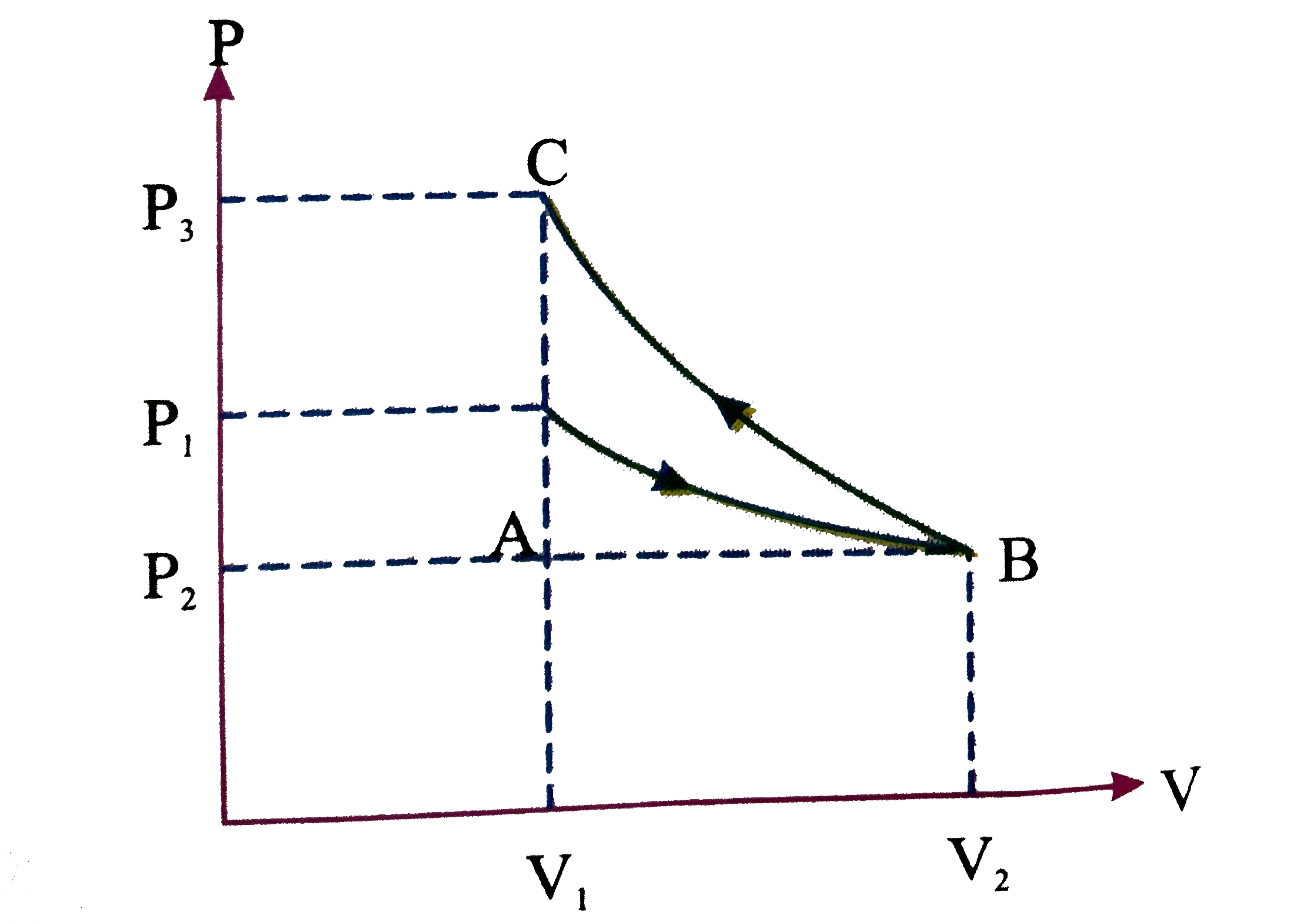
The workdone W is positive if volume increases in the process and W is negative if volume decreases in the process. Hence WAB is positive as volume increases from V1→V2 , WBC is negative as volume decrases from V2→V1 .
Further |WBC|>|WAB|
Net workdone =WAB+(−WBC)
W=A negative value (∴|WBC|>|WAB|)orW<0 From the graph itself, P3>P1
∴W<0andP3>P1
Hence option (c) repesents correct answer.
Topper's Solved these Questions
Similar Questions
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
If P3 and P2 are equal, thenView SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which relation is correct (γ=CPCV)?View Solution
Knowledge Check
- Question 1 - Select One
An ideal gas expands isothermally from volume V1 to V2 and is then compressed to original volume V1 adiabatically. Initialy pressure is P1 and final pressure is P3. The total work done is W. Then
AP3>P1,W>0BP3<P1,W<0CP3>P1,W<0DP3=P1,W=0 - Question 2 - Select One
An ideal gas of volume V and pressure P expands isothermally to volume 16 V and then compressed adiabatically to volume V . The final pressure of gas is [γ=1.5]
APB3PC4PD6P - Question 3 - Select One
A gas expands under constant pressure P from volume V1 toV2The work done by the gas is
AP(V2−V1)BP(V1−V2)CP(Vλ1−Vλ2)DPV1V2V2−V1
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which graphic representation is correct
a.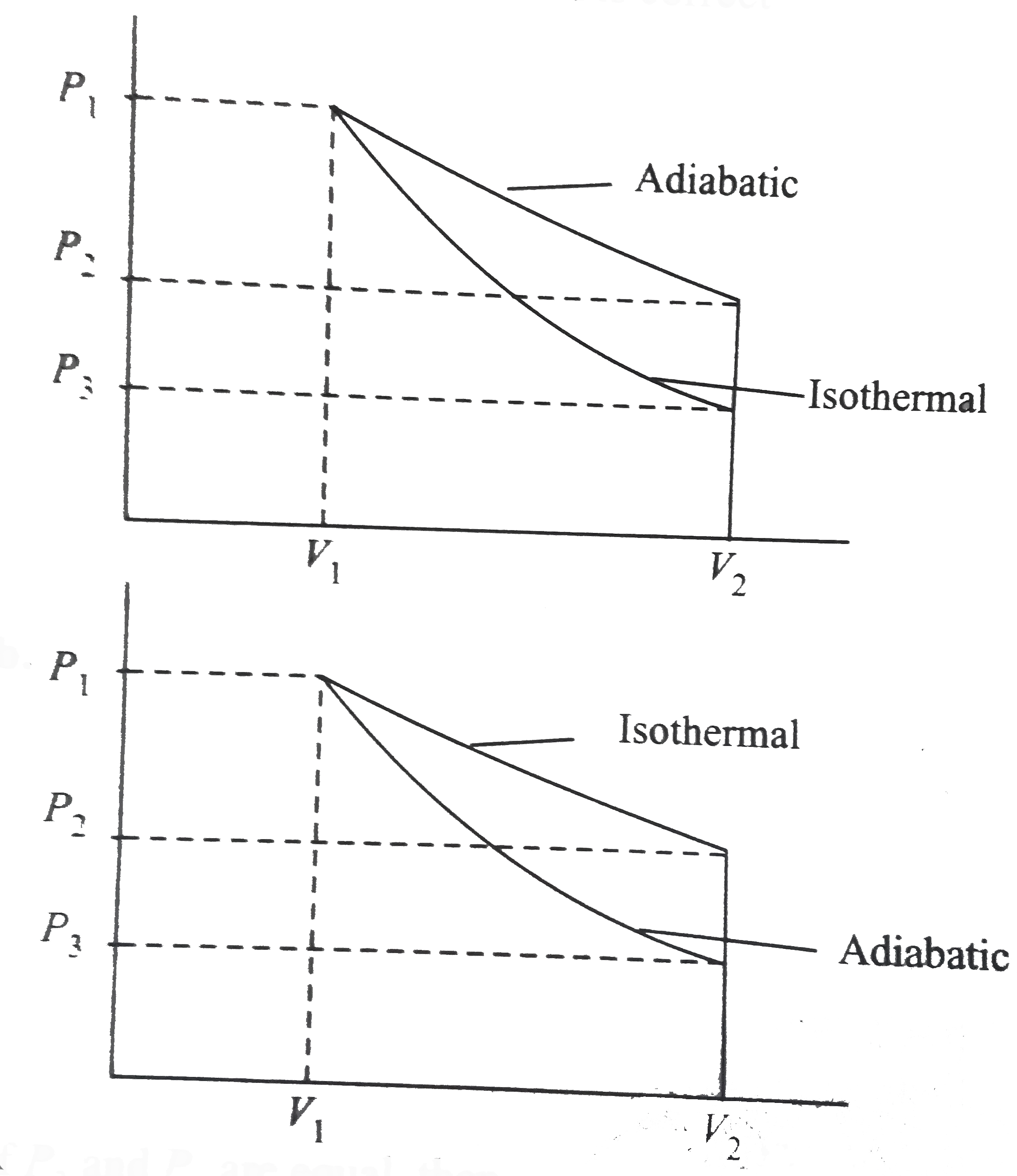 View Solution
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
The work of expansion in adiabatic process (wadi) is related to work of expansion in isothermal process (wiso) isView SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which of the following is correct?View SolutionFor an ideal gas with initial pressure and volume Pi and Vi, respectively, a reversible isothermal expansion happers, when its volume becomes V0. Then it is compressed to its original volume Viby a reversible adiabatic process. If the final pressure is Pf, then which of the following statement is true?
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure P1. The same gas is expanded adiabatically to a volume 2V, the final final pressure is PA. In terms of the ratio of the two specific heats for the gas γ, the ratio PI/PA is
View Solution

