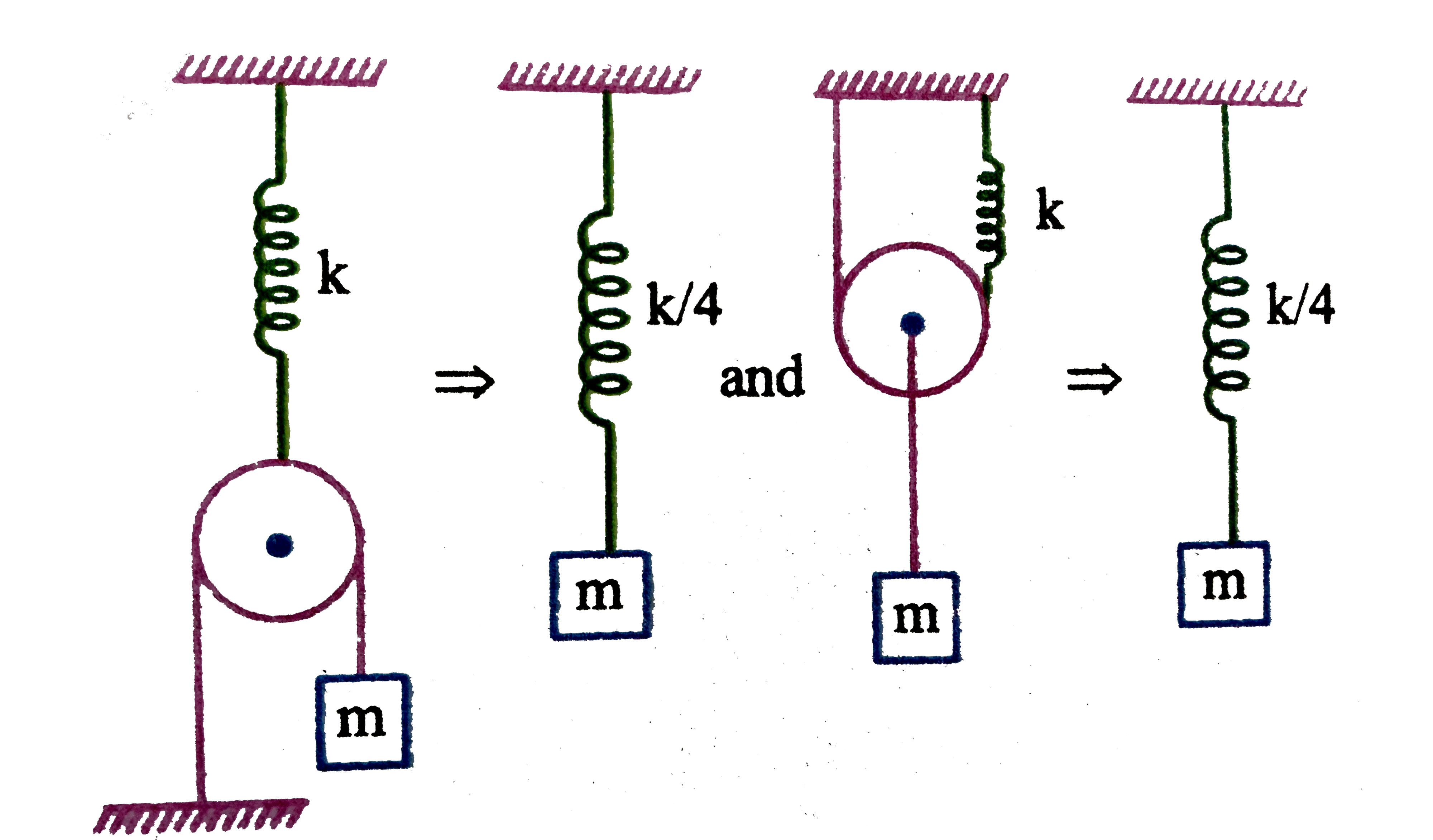
The time periods of system depicted below under identical conditions are respectively.
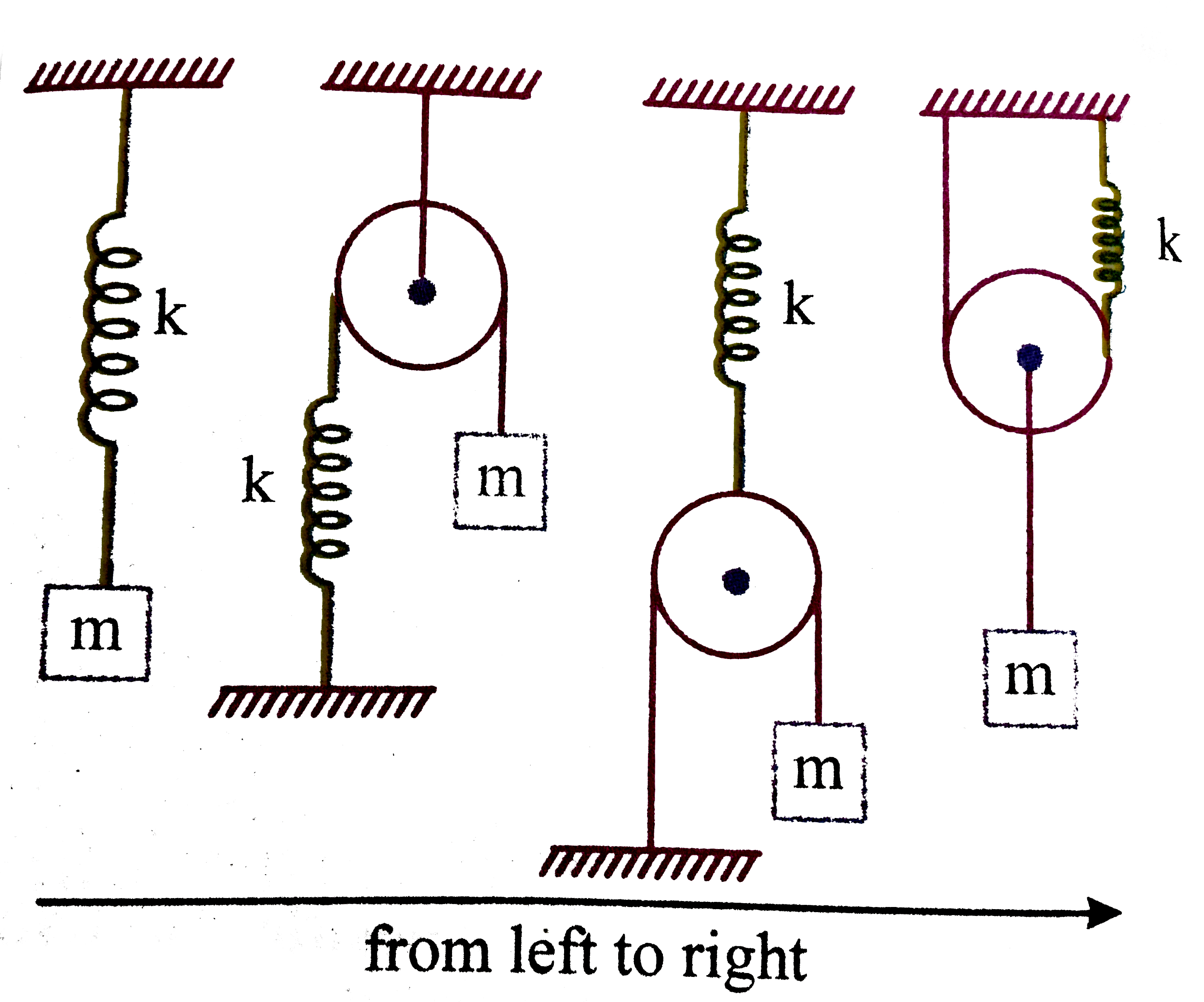
(i) 2π√mk, (ii) 2π√4mk, (iii) 2π√m4k
ii,i,ii,iii
i,ii,iii,ii
i,ii,ii,iii
i,i,ii,iii
The correct Answer is:D
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage
33 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
The acceleration due to gravity on the surface of earth is 9.8ms−2.Time period of a simple pendulum on earth and moon are 3.5 second and 8.4 second respectively. Find the acceleration due to gravity on the moon .
Hint :Te=2π√LgeTm=2π√Lgm
T2eT2m=gmge
gm=T2eT2mge
View Solution[" Uncertainty in measuring speed of a "],[" particle is numerically equal to "],[" uncertainty in measuring its position."],[" The value of these uncertainties will "],[" be "],[" (1) equal to "sqrt((h)/(4 pi m))],[" (2) less than "sqrt((h)/(4 pi m))],[" (3) greater than "sqrt((h)/(4 pi m))],[" (4) (1) or (3) "]
View SolutionIn each of the following cases find the period of the function if it is periodic.
(i) f(x)=sinπx√2+cosπx√3 (ii) f(x)=sinπx√3+cosπx2√3
View SolutionProve that (i) sin .π6. cos .π6=√34 (iii)cos2.π2−sin2.π2=√32
View SolutionWhat is the simplified value of ⎡⎣4m+14×√2×2m2√2−m⎤⎦1m?
View SolutionIf ∫∞0e−x2 dx=√π2, and ∫∞0e−ax2 dx, a>0 is (i) √π2 (ii) √π2a (iii)2√πa (iv) 12√πa
View SolutionThe vertical motion of a huge piston in a machine is approximately SHM. A block of 5 kg is placed on the piston. The maximum amplitude of the piston's SHM for the block and the piston to remains together is 0.99m. Find the frequency .
Hint : v=12π√km
Find k
For maximum displacement xmax=A
For maximum restoring force , F=−kA=−mg
∴k=mgA. Put the valeu of K in v=12π√km to find v .
View SolutionIf(4+√15)32−(4−√15)32=k√6, then k is
View SolutionThe angle of rotation of axes so that √3x−y+1=0 transformed as y=k is (i)π6 (ii)π4 (iii)π3 (iv)π2
View Solutionlimx→1−√π−√2sin−1x√1−x= (A) √2π (B) √π2 (C) 1π (D) √1π
View Solution