A thin-walled tube of mass m and radius R has a rod of mass m and vry small cross section soldered on its inner surface. The side-view of the arrangement is as shown in the following figure. The entire arrangement is placed on a rough horizontal surface. The system is given a small angular displacement from its equilibrium position, as a result, the system performs oscillations. The time period of resulting oscillations if the tube rolls without slipping is
2π√4Rg
2π√2Rg
2π√Rg
None of these
The correct Answer is:A
Rolling can be considered as pure rotation about point of contact, P: Now it is compound pendulum oscillating about 'P'.

∴T=2π√Imgd, where I=mR2+mR2=2mR2.
d=R/2∴T=?
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I2videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage33videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mK - Question 2 - Select One
A system is shown in the figure. The force The time period for small oscilations of the two blocks will be
 A2π√3mKB2π√3m2KC2π√3m4KD2π√3m8K
A2π√3mKB2π√3m2KC2π√3m4KD2π√3m8K - Question 3 - Select One
A rectangular block of mass m and area of cross a small vertical displacement from equilibrium it undergoes oscillation with a time period T then
AT∝√pBT∝1√ACT∝1pDT∝1√m
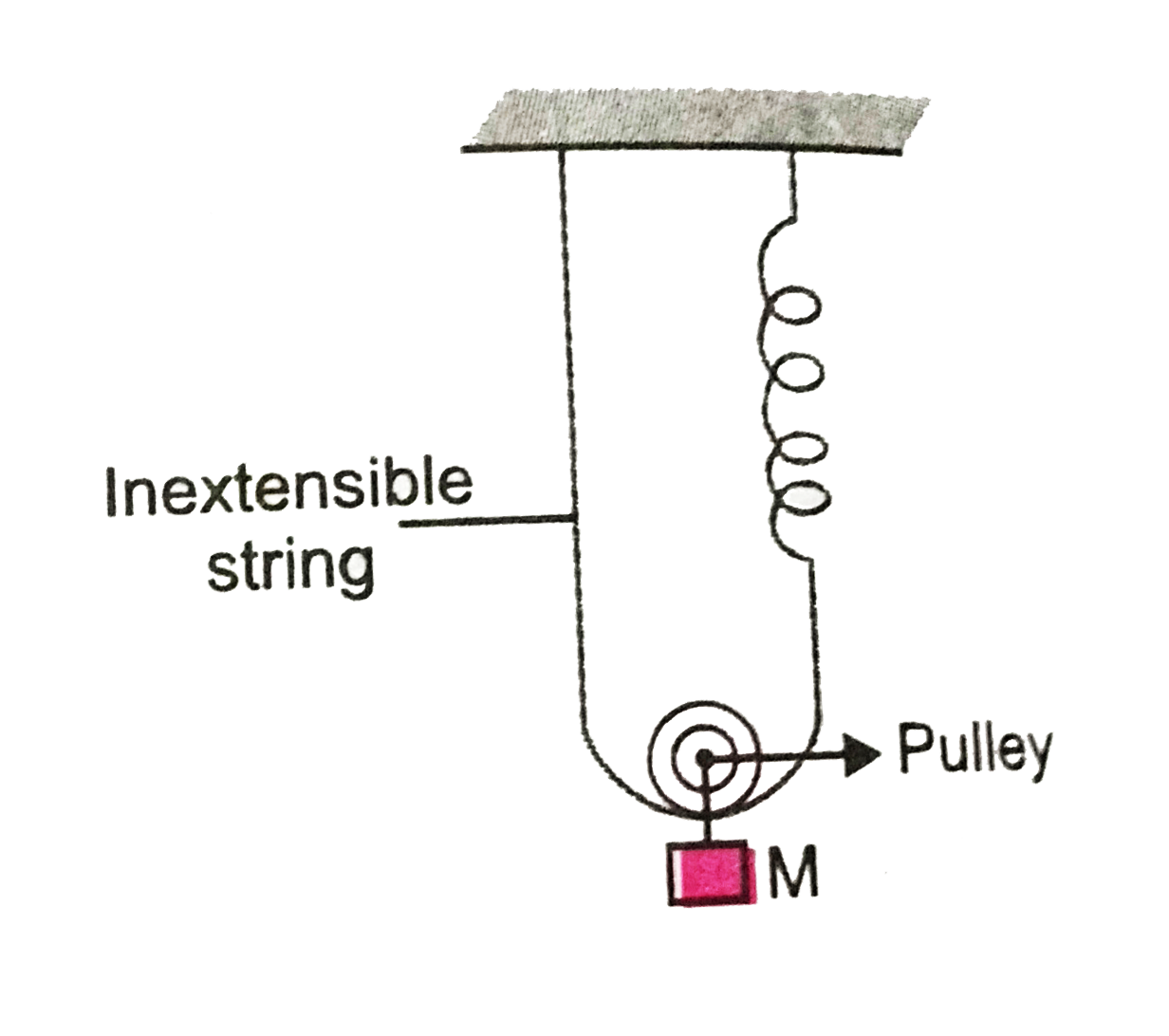
In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.
 View Solution
View SolutionA small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png) View Solution
View SolutionA thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View Solution