A body A of mass m1 and body B of mass m2 are interconnected by a massless spring as shown. The body A performs free vertical harmonic oscillations with the amplitude A and frequency f. The maximum value of f such that body B does not leave the surface is

12π√(m1+m2m2)gA
12π√(m1+m2m1)gA
12π√gA
12π√m2m1.gA
The correct Answer is:B
As A oscillates up and down, the normal force between B and surface varies from minimum to maximum. To keep body B in contact with the surface, the Rminimum≥0 and R becomes minimum, when A is at topmost position. Free body diagrams are:
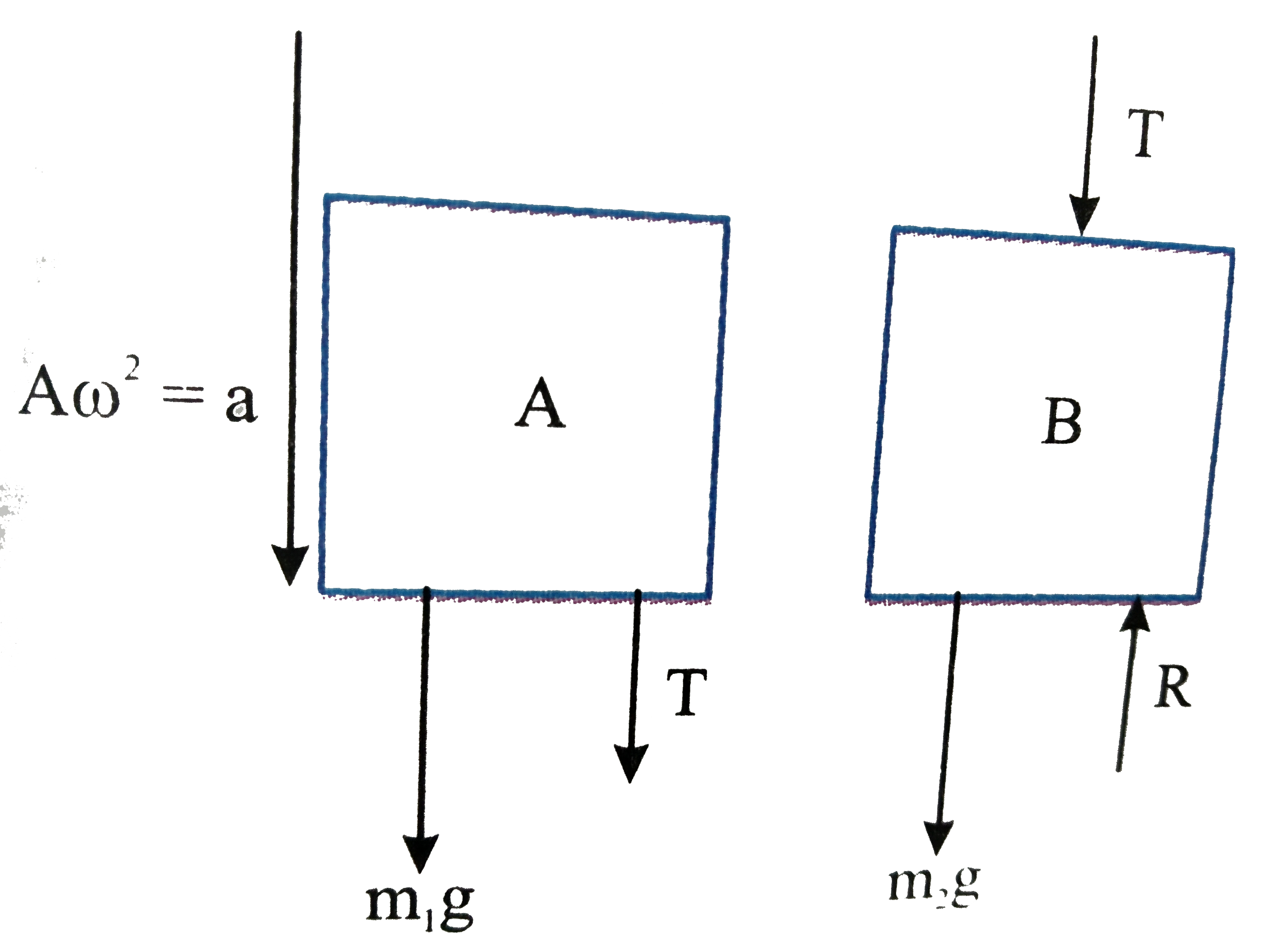
T+m1g=m1Aw2.............(1)
−T+m2g=R..........(2)
and R≥0...............(3)
solve for fmin=?
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage
33 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A body A mass m1=1kg and body B of mass m2=4.1kg. The body A perform free vertical harmonic oscillations with the amplitude 1.6cm and frequency 25Hz. Neglecting the mass of the spring , find the maximum and m inimum value of force that the system exerts on the hearing surface.

View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View Solution
Knowledge Check
A body is vibrating in simple harmonic motion with an amplitude of 0.06 m and frequency of 15 Hz . The velocity and acceleration of body is
A5.65m/sand5.32×102m/s2B6.82m/sand7.62×102m/s2C8.91m/sand8.21×102m/s2D9.82m/sand9.03×102m/s2A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3KmFor a body of mass m attached to the spring the spring factor is given by
Am/ω2Bmω2Cm2ωDm2ω2
A body A of mass m1=1kg and a body B of mass m2=4kg are attached to the ends of a spring. The body A performs vertical simple harmonic oscillations of amplitude a=1.6cm and angular frequencyomeg=25rads. Neglecting the mass of the sppring determine the maximum and minimum values of force the system exerts on the surface on which in rests.
[Take g=10m/s2]

View SolutionA body of mass 2m is connected to another body of mass m as shown in figure. The mass 2m performs vertical S.H.M. Then find out the maximum amplitude of 2m such that mass m doesn't lift up from the ground.
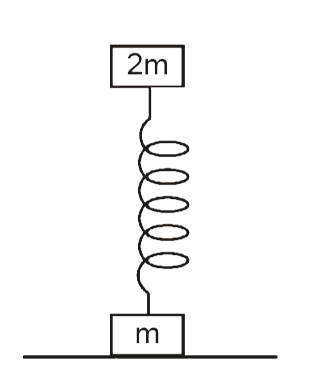
View SolutionTwo mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View Solution" The potential energy of a body of mass "m" on the surface of earth is "
View SolutionTwo bodies A and B each of mass M are fixed together by a massless spring A force F acts on the mass B as shown in fig At the instant shown the mass A has acceleration a. What is the acceleration of mass B?

View Solution
