Two identical simple pendulums each of length 'l' are connected by a weightless spring as shown. In equilibrium, the pendulums are vertical and the spring is horizontal and undformed. The time period of small oscillations of the linked pendulums, when they are deflected form their equilibrium positive through equal displacements in the same vertical plane in the opposite directions and released, is

2π√lg
2π ⎷l(g+2klm)
2π ⎷l(g+klm)
2π√2lg+mk
The correct Answer is:B
At the disturbed position:
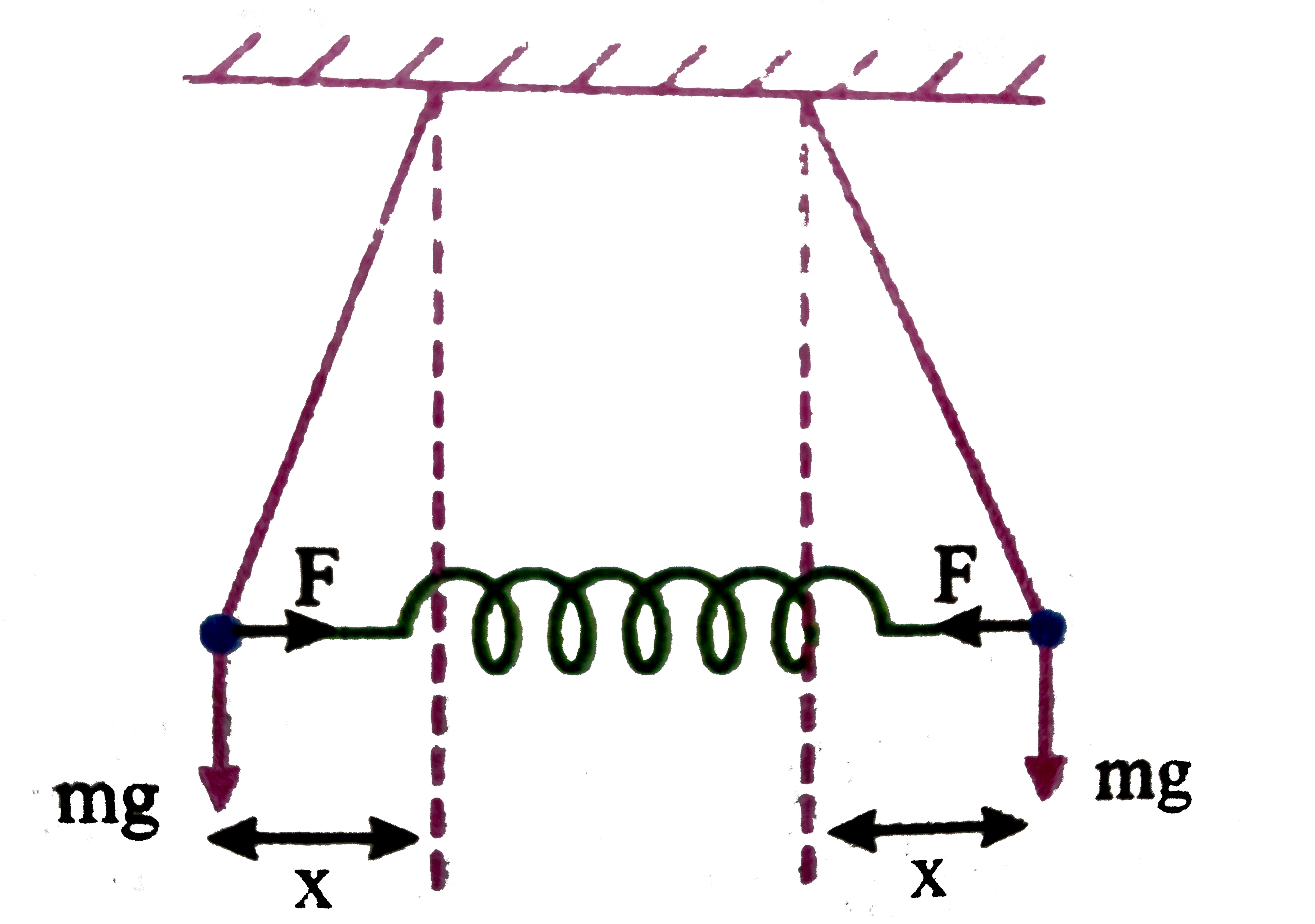
Restoring torque on particle is
τ=−[(mg×lsinθ)+(2klθ×lcosθ)]
for small, θ,sinθ→θ:cosθ→1 and
τ=Iα,α=−ω2θ:T=2πω
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I2videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage33videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
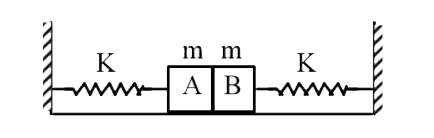 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
At=2π√l/gBt=2π√lcosθ/gCT=4π2mlt2DThe bob is in equilibrium - Question 2 - Select One
A simple pendulum has length L and period T. As it passes through its equilibrium position, the string is suddenly clamped at its midpoint. The period then becomes
A2TBTCT2Dnone of these - Question 3 - Select One
A simple pendulum bob has a mass ''m'' and length ''L''. The bob is drawn aside such that the string is horizontal and then it is released. The velocity of the bob while it crosses the equilibrium position is
A√gLB√2gLC√5gLD√3gL
A uniform rod of length l is suspended by end and is made to undego small oscillations. Find the length of the simple pendulum having the time period equal to that of the rod.
View SolutionConsider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.
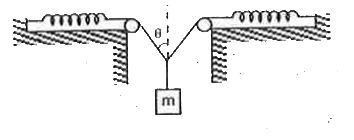 View Solution
View SolutionA simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
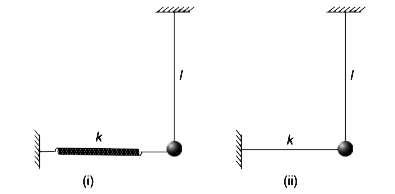 View Solution
View SolutionTwo identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (useg=9.8m/s2)
 View Solution
View SolutionA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
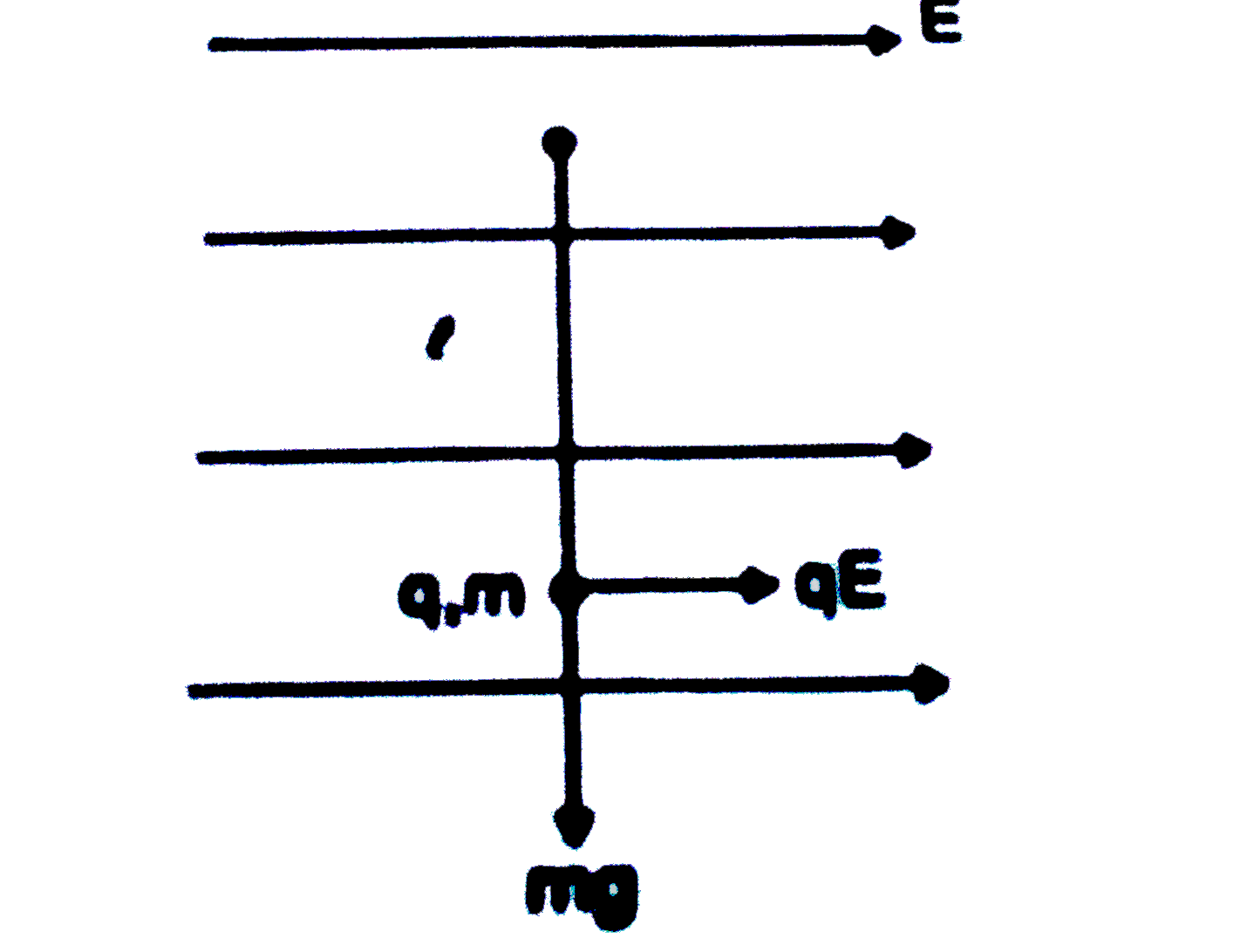 View Solution
View Solution

