The block shown in figure has a mass M and descends with an acceleration a. the mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.

Consider the block +the part of the string below A'' as the system . Let the tension at A be T. The forces acting on this system are
a. (M+mg)g, downward, by the earth
T, upward, by the upper part of the string.
The first is gravitatioN/Al and the second is electromagnetic. We do not have to write the force by the string on the block. This electromagnetic force is by one part of the system on the other part. Only the forces acting on the system by the objects other than the system are to be included.
The system is descending with an acceleration a. Taking the downward direction as the X-axis, the total force along the X-axis is (M+m)g−T. Using Newton's law along the X-axis is (M+mg)g−T=(M+m)a.
or T=(M+m)(g−a)
we have omitted the free body diagram. This you can do if you can draw the free body diagram in your mind and write the equations correctly.
To get the tension T' at the lower end we can put m=0∈i.
Effectively we take the point A at the lower end. Thus, we get T'=M(g−a).
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Worked Out Examples
11 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Short Answer
17 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgA mass m is revolving in a vertical circle at the end of a string of length 20 cm. By how much does the tension of the string at the lowest point exceed the tension at the top most point?
A2 m gB4 m gC6 m gD8 m g
A mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
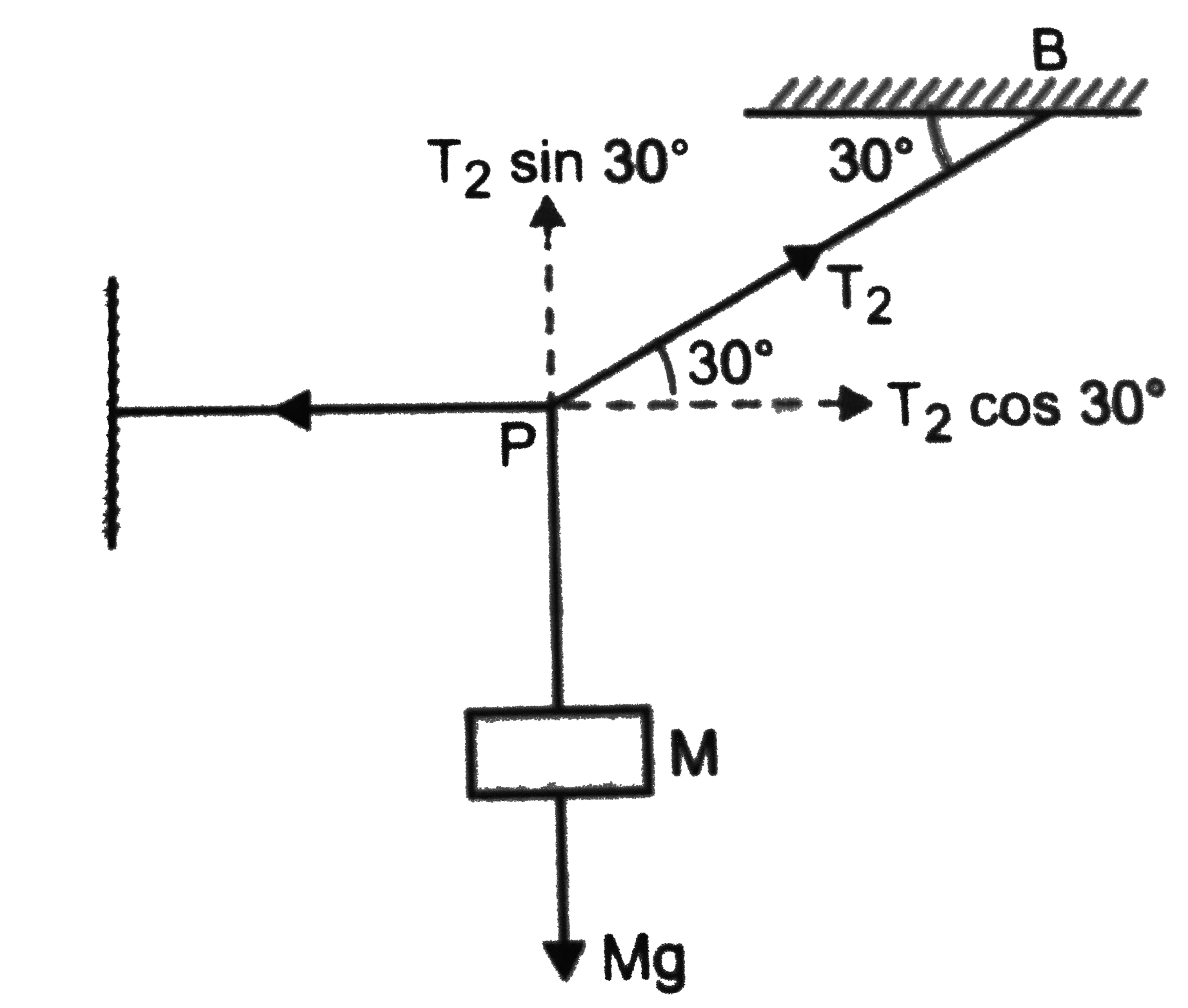
View SolutionA thin uniform bar of mass m and length 2L is held at angle 30∘ with the horizontal by means of two vertical inextensible strings, at each and as shown in figure. If the string at the right end breaks, leaving the bar to swing the tension in the string at the left end of the bar immediately after string breaks is T=n13mg

View SolutionAs shown in the figure, two blocks, each of mass m, suspended from the ends of a rigid light rod of length L. The rod is held horizontally on the fulcrum and then released.
(a) Find the initial angular acceleration of the rod.
(b) If the mass of rod is also m uniformly distributed. find the tension in the strings attached to blocks.

View SolutionConsider4 the situation shown in figure. Bothe the pulleys and the string are light and all the surfaces are friction less. a. Find the acceleration of the mass M. b. Find the tension in the string c. Calculate the force exerted by the clamp on the pulley A in the figure.

View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionA block of mass M is being pulled with the help of a string of mass m and length L. the horizontal force applied by the man on the string is F.

Determine
(a) Find the force exerted by the string on the block and acceleration of system.
(b) Find the tension at the mid point of the string.
(c ) Find the tension at a distance x from the end at which force is applied.
Assume that the block is kept on a frictionless horizontal surface and the mass is uniformly distributed in the string.
View Solution

