Accelertion of block m is (θ<45∘)
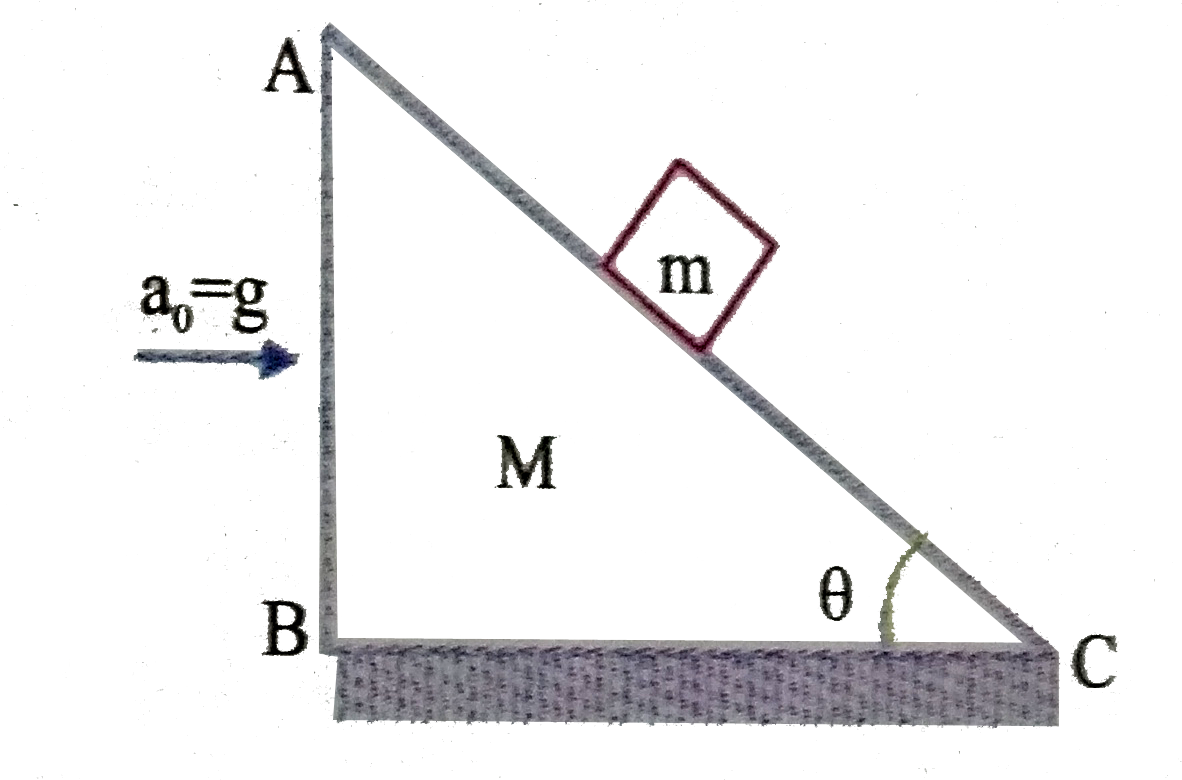
gsinθ
gcosθ
g(cosθ+sinθ)
g(cosθ−sinθ)
The correct Answer is:D
FR=mgcosθ−mgsinθ
Topper's Solved these Questions
Similar Questions
In the figure shown, angle of repose is 45∘.Find force of friction, net force and acceleration of the block when
(a) θ=30∘ (b)θ=45∘ (c)θ=60∘
View SolutionConsider the following statements :
1. If 45∘<θ<60∘, then sec2θ+cosec2θ=α2 for some real number α>1.
2. If 0∘<θ<45∘, then 1+cosθ1−cosθ=x2 for some real number x>2.
3. If 0∘<θ<45∘, then cosθ1−tanθ+sinθ1−cotθ≥2.
What is the number of true statements ?
View Solution
Knowledge Check
Acceleration of block m is (θ<45∘)
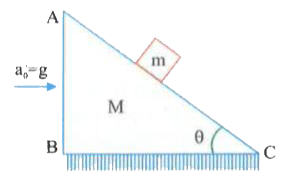 AgsinθBgcosθCg(sinθ−cosθ)Dg(cosθ−sinθ)
AgsinθBgcosθCg(sinθ−cosθ)Dg(cosθ−sinθ)Let αandβ be the roots of the quadratic equation
x2sinθ−x(sinθcosθ+1)+cosθ=0
(0<θ<45∘)andα<β. Then
∞∑n=0(αn+(−1)nβn) is equal to :A11−cosθ−11+sinθB11+cosθ+11−sinθC11−cosθ+11+sinθD11+cosθ−11−sinθA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
Amg cos θBmgCmg sin θDNone of these
In the previous problem ,find the magnitude of change in velocity if (a) 90∘<θ<180∘ , (b) 180∘<θ<270∘ and (c ) 270∘<θ<360∘.
View SolutionA block of mass m is placed on a wedge of mass M. Coefficient between then is μ<cotθ. The wedge is given an acceleration to its left. Find the maximum acceleration at which block apears stationary relative to wedge.

View SolutionWhat is the value of θ,0∘<θ<90∘, if cosθ+sinθ=√2?
View SolutionFor 0<θ<π2, the solutions of σ6m−1cosec(θ+(m−1)π4) cosec (θ+mπ4)=4√2 is (are):
View SolutionIf sinθ=√3cosθ,0<θ<90∘ , then θ is equal to .
View Solution
