Two identical beam A and B of plane coherent waves of the sasme intensity and wavelength λ fall on a plane screen. The direction of the beam propagations make angles θ1 and θ2 with the normal to the screen and lie in the same plane as shown in the figure. Find the distance β between adject interfrence fringes on the screen.

λsinθ−sinθ2
λsinθ1+sinθ2
λ(sinθ1−sinθ2)sinθ1+sinθ2
λ(sinθ1+sinθ2)sinθ1−sinθ2
The correct Answer is:A
Let P be the central bright fringe

Path difference between A 'P' and B'P' is
Δx=ysinθ1−ysinθ2
Δx=y(sinθ1−sinθ2)
For bright fringes Δx=nλ
nλ=y(sinθ1−sinθ2)
y=nλsinθ1−sinθ2
∴β=λsinθ1−sinθ2
Topper's Solved these Questions
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - I(H.W)
20 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II(H.W)
19 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - V
37 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
19 Videos
Similar Questions
A plane monochromatic light wave with wavelength λ falls on the surface of a glass wedge whose faces from an angle α<<1. The plane of incidence is perpendicualr to the edge, the angle of incidence is θ1. Find the distance between the neighbouring fringe maxima on the screen placed at right angles to reflected light.
View SolutionA beam with wavelength λ falls on a stack of partially reflecting planes with separation d. The angle θ that the beam should make with planes so that the beams reflected from successive planes may interfere constructively is (where n=1, 2, ...)
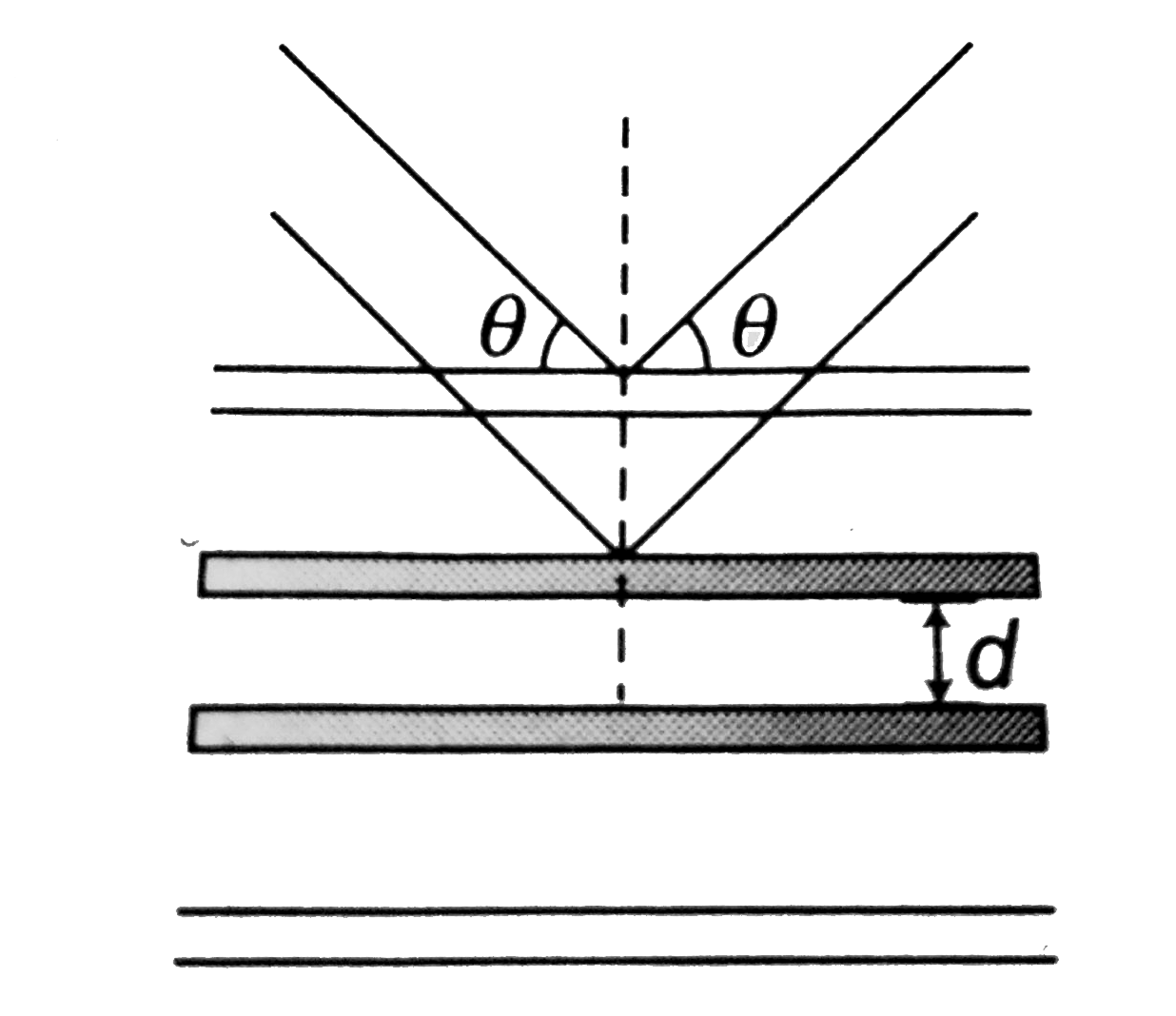
View Solution
Knowledge Check
Two identical beam A and B of wavelength λ fall cylindeical screen. The angle between the directions a point P on the screen at angular position ϕ from the beam A as shown in the figure. Find the distance between adjacent interference fringes on the screen near the point P. Asume that the distance β between adjacent fringes is much less than the radius of the cylinder.
 Aλ2sin(ϕ2)cos(θ−ϕ2)Bλ2sin(ϕ2)cos(θ+ϕ2)Cλ2sin(θ2)cos(θ+ϕ2)Dλ2sin(θ2)cos(ϕ+θ2)
Aλ2sin(ϕ2)cos(θ−ϕ2)Bλ2sin(ϕ2)cos(θ+ϕ2)Cλ2sin(θ2)cos(θ+ϕ2)Dλ2sin(θ2)cos(ϕ+θ2)Monochromatic light waves of wavelength λ from two coherent source fall on a larger plane screen. One of the waves is emanated from a point source S located at distance L from the screen and the other one is a broad plasne wave as shown in the figure. The spacing between the nth and (n−1)th bright fringe is
 A√2λL(√n−√n−1)B√λL(√n−√n−1)Cλ22L(√n−√n−1)D2λ2L(√n−√n−1)
A√2λL(√n−√n−1)B√λL(√n−√n−1)Cλ22L(√n−√n−1)D2λ2L(√n−√n−1)A beam with wavelength λ falls on a stack of partially reflecting planes with separation d. The angle θ that the beam should make with planes so that the beams reflected from successive planes may interfere constructively is (where n=1, 2, ...)
 Asin−1(nλd)Btan−1(nλd)Csin−1(nλ2d)Dcos−1(nλ2d)
Asin−1(nλd)Btan−1(nλd)Csin−1(nλ2d)Dcos−1(nλ2d)
A beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
View SolutionA beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
View SolutionA parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Show that if the incident beam makes an angle θ=sin−1(λ2d) with the normal to the plane of the slits, there will be a dark fringe at the centre Po of the pattern.
View SolutionA beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
View SolutionIf two coherent source are placed at a distance 3λ from each other, symmetric to the centre of the circel as shown in figure, Find thenumber of fringes shown on the screen, placed along the circumference ?

View Solution
