A transparent slab of thickness t and refractive index μ is inserted in front of upper of YDSE apparauts. The wavelength of ligth used. is λ. Assume that there is no absorption of light by the slab. Mark the correct statement(s).
The intensity of dark fringes will be zero, if slits are identical.
The change in optical path due to insertion o9f palte is μt .
The change in optical path due to insertion of plate is (μ−1)t .
For making intensity zero at centre of screen the thickness can be 5λ2(μ−1).
The correct Answer is:A, C, D
Solution: Path difference at 'P'
Δx=(S1P−t)air+tmed−S1Pair
=S1P−S2P−t+μtΔx=(S1P−S2P)+(μ−1)t

When there is no absorption of light by slab then path difference at P earlier is S1P−S2P=0 . so change in optical path due to inserion of slab is (μ−1)t .
For Intensity to be zero at 'P' we have Δx=(2n−1)λ2=(μ−1)t⇒t=(2n−1)λ2(μ−1)
Then t=λ2(μ−1),3λ2(μ−1),5λ2(μ−1) , - - - - -
Topper's Solved these Questions
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - I(H.W)
20 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II(H.W)
19 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - V
37 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
19 Videos
Similar Questions
In Young’s double slit experiment a monochromatic light of wavelengthλ from a distant point source is inci- dent upon the two identical slits.The interference pattern is viewed on a distant screen. Intensity at a point P is equal to the intensity due to individual slits (equal toI0). A thin piece of glass of thickness t and refractive index μ is placed in front of the slit which is at larger distance from point P, perpendicular to the light path. Assume no absorption of light energy by the glass.
(a) Write intensity at point P as a function of t.
(b) Write all values of t for which the intensity at P is minimum.
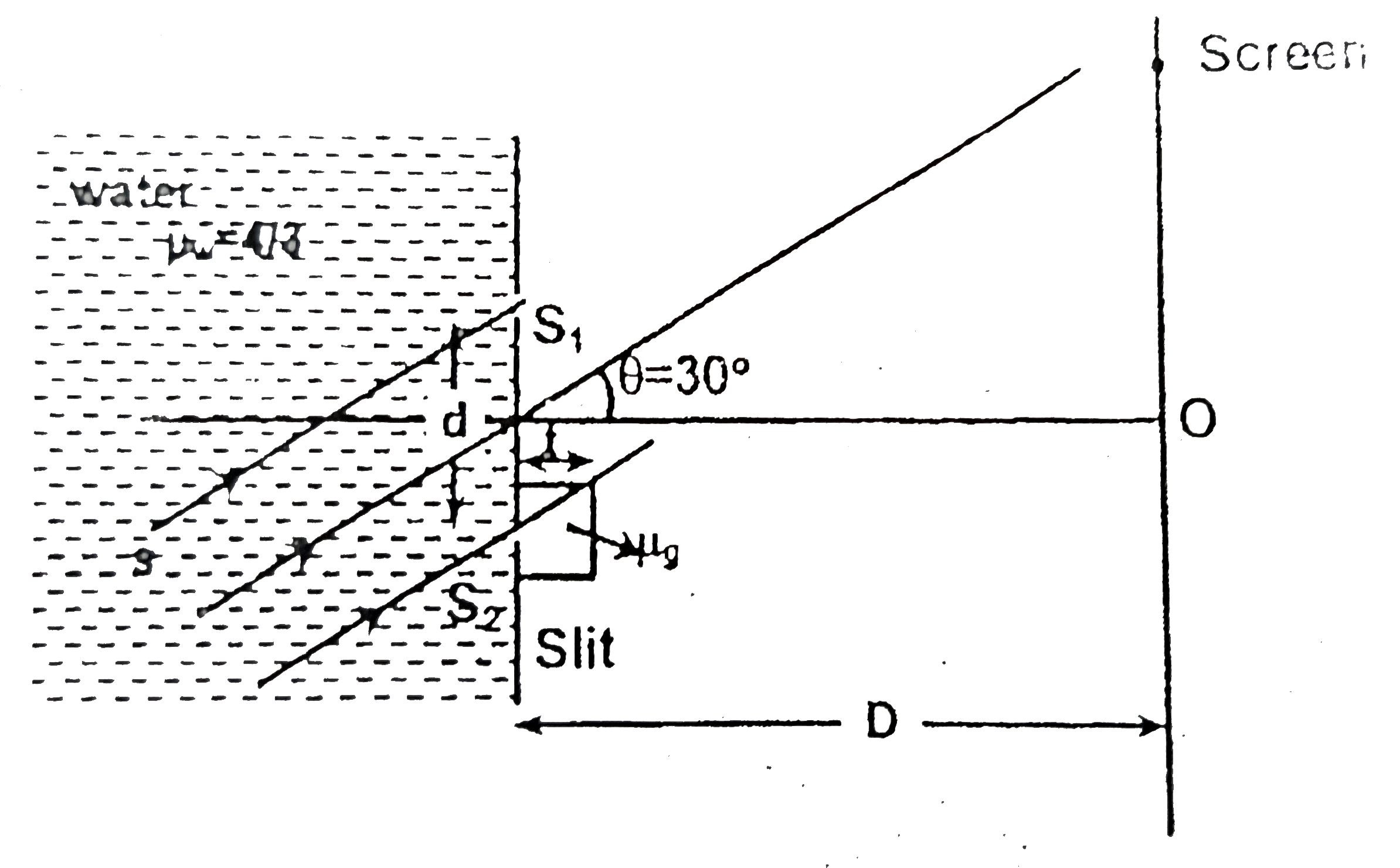
View SolutionIn a YDSE experiment the two slits are covered with a transparent membrane of negligible thickness which allows light to pass through it but does not allow water. A glass slab of thickness t=0.41mm and refractive index μg=1.5 is placed infront of one of the slits as shown in the figure. The separation between the slits is d=0.30mm. The entire space to the left of the slits is filled with water of refractive index μw=4/3.
A coherent light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1m from the slits, find
(a) the position of central maxima.
(b) the intensity at point O.
View Solution
Knowledge Check
When a transparent parallel plate of uniform thickness t and refractive index μ is interposed normally in the path of a beam of light, the optical path is
Aincreased by μtBdecreased by μtCdecreased by (μ−1)tDincreased by (μ−1)tIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
Aλ(2μ−1)B2λ(2μ−1)Cλ(μ−1)D2λ(2μ+1)When a thin transparent plate of thickness t and refractive index μ is placed in the path of one the two interfering waves of light, then the path difference changes by
A(μ+1)tB(μ−1)tC(μ+1)tD(μ−1)t
In YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
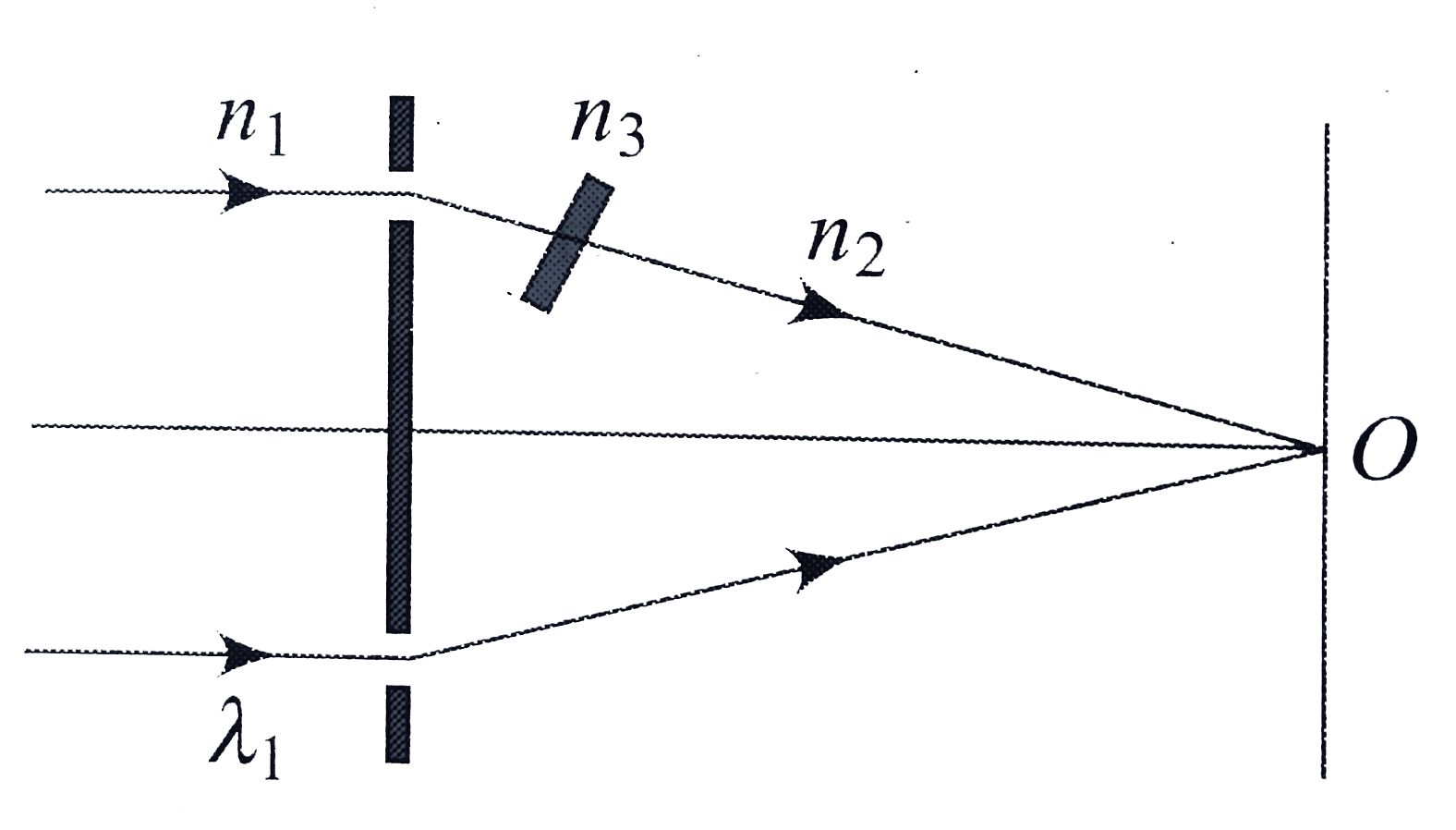
View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
View SolutionA transparent sheetof refractive index 1.5 is kept near one of the slits of the YDSE apparentus. The intenisity at the centre of the screen (where the central maximum was located before the introduction of the sheet) is half of the previous value. The minimum thickness of the sheet should be (wavelength of the monochromatic light used in the experiment is 6000Å) :
View SolutionA transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1andn2(>n1), as shown in the figure. A ray of light is incident with angle θi, from medium 1 and emerges in medium 2 with refraction and θf, with a lateral displacement l.
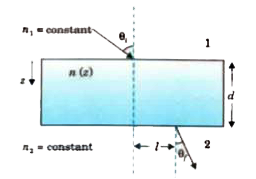
Which of the following statement(s) is (are) true ?
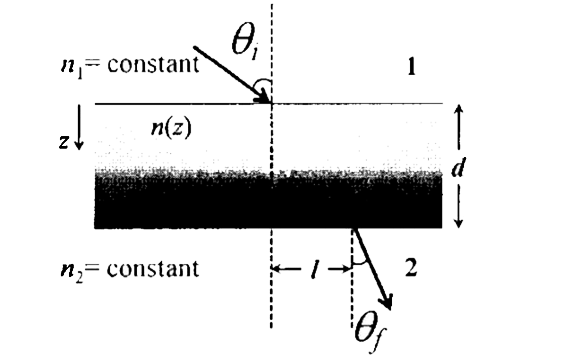
View SolutionA transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1 and n2(>n1), θi, from medium 1 and emerges in medium 2 with refraction angle θfwith a lateral displacement l.
Which of the following statement(s) is (are) true?
View Solution
