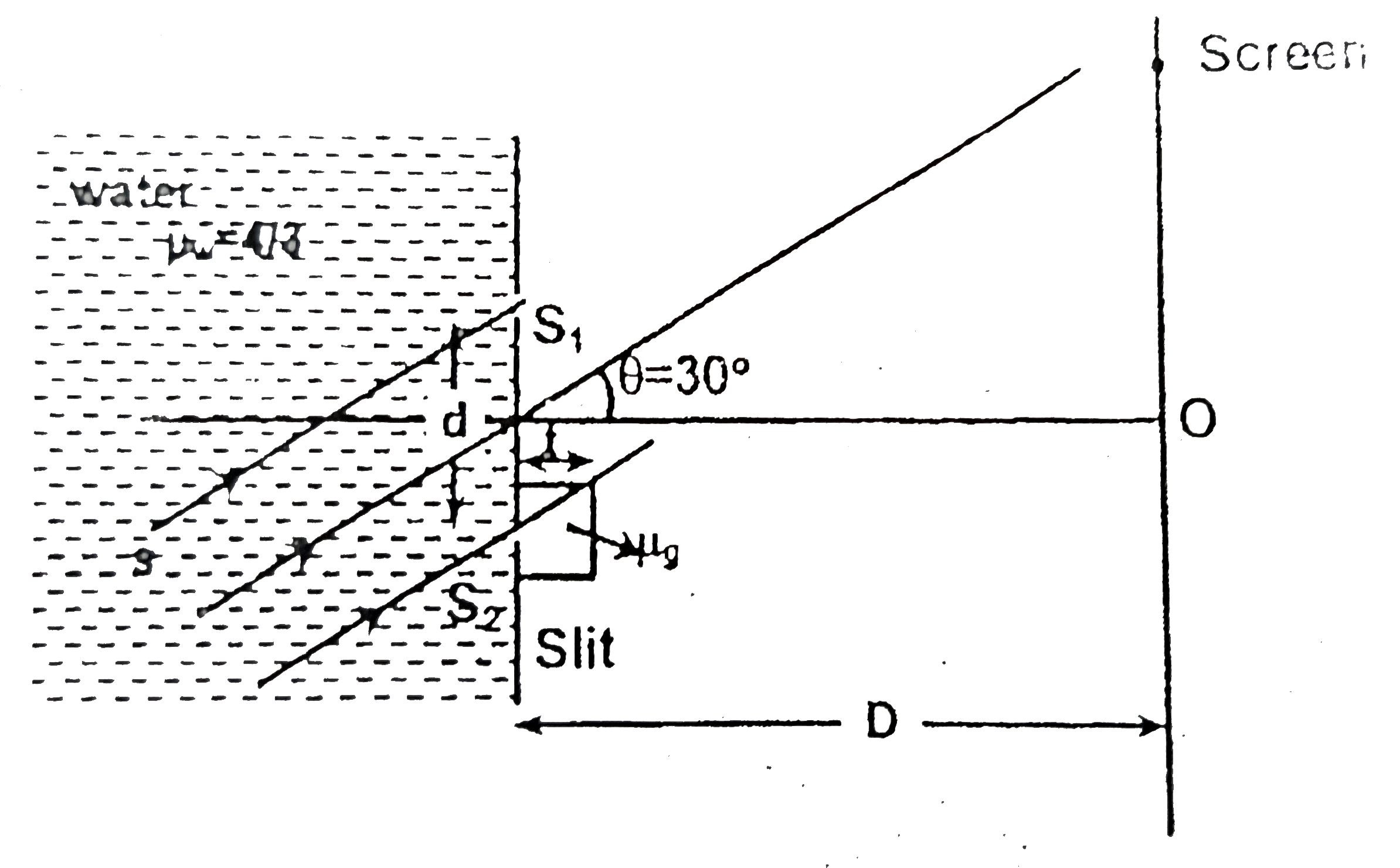
In a YDSE experiment the two slits are covered with a transparent membrane of negligible thickness which allows light to pass through it but does not allow water. A glass slab of thickness t=0.41mm and refractive index μg=1.5 is placed infront of one of the slits as shown in the figure. The separation between the slits is d=0.30mm. The entire space to the left of the slits is filled with water of refractive index μw=4/3.
A coherent light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1m from the slits, find
(a) the position of central maxima.
(b) the intensity at point O.
(a) Let central maxima lies at point P at a distance x from the central line. Then optical path difference Δp at point P is
(S2P−t)+tμg−μwdsinθ−S1P
⇒S2P−S1P+(μg−1)t−μqdsinθ
⇒xdD+(μg−1)t−μwdsinθ
For central maxima Δp=0
x=Dd[(μwdsinθ)−(μg−1)t]
=13×10−4[43×3×10−4×12−0.5×0.41×10−3]
=13×10−4[2×10−4−2.05×10−4]=−5×10−63×10−4
=−1.66×10−2m=−1.66cm
Central maxima lies at a distance 1.66cm below the central line
(b) At point O, optical path difference is
(μg−1)t−μwdsinθ=−5×10−6m
So intensity at O
I0=I+I+2√IIcos2π5×10−7(−5×10−6)
I0=4I

Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Objective problems
215 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
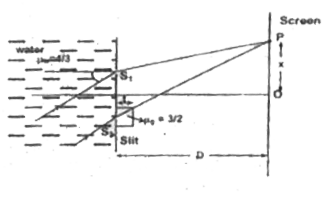
A coherent beam light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1 m from the slits and the separation between- the slits is 3×10−4m. A thin film of glass μg= 3/2 and thickness 0.41 mm is placed near one slit as shown in the figure, find
(a) the position of central maxima.
(b) the intensity at'point O.
View SolutionA plate of thickness t made of material of refractive index μ is placed in front of one of the slits in a double slit experiment . What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ?
View Solution
Knowledge Check
In YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
Aλ(2μ−1)B2λ(2μ−1)Cλ(μ−1)D2λ(2μ+1)In YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
Aβ(μ−1)t2λBβ(μ−1)tλCβ(μ−1)t3λDβ(μ−1)t4λIn biprism experiment the fringe width is 0.30mm. If slits are covered by glass plate of thickess 0.04 mm and refractive index μ=1.5 then the fringe widht is
A0.02mmB0.1mmC0.30mmD0.2mm
In the YDSE shown the two slits are covered with thin sheets having thickness t&2t and refractive index 2μand μ .Find the position (y) of central maxima.

View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
View SolutionIn YDSE experiment separation between plane of slits and screen is 1m. Separation between slits is 2mm. The wavelength of light is 500nm. The fringe width is
View SolutionA thin perfectly transparent glass sheet of thickness t and refractive index mu is pasted on one of the two identical slits. If the intensity of light at the centre of the screen is I0 in the absence of glass sheet, the intensity at O as a function of thickness of the glass plate is
View SolutionIn a young's double slit experiment ,let Aand B be the two slits.A thin film film of thickness t and refractive indexμ is pklaced in front of A.Let β =fringe width.The central maximum will shift:
View Solution