In $Δ A B C$ prove that $A B^{2} + A C^{2} = 2 (A O^{2} + B O^{2})$ ; where O is the middle point of BC.

Video Solution

|

Answer

Step by step video & image solution for In DeltaABC prove that AB^2+AC^2=2(AO^2+BO^2); where O is the middle point of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS COORDINATE GEOMETRY

Similar Questions

In $A B C$ Prove that $A B^{2} + A C^{2} = 2 (A O^{2} + B O^{2})$ , where $O$ is the middle point of $B C$
View Solution
In any triangle ABC, prove that $A B^{2} + A C^{2} = 2 (A D^{2} + B D^{2})$ , where D is the midpoint of BC.
View Solution
in $Δ A B C, ∠ A = 2 ∠ B$ Prove that $B C^{2} = A C^{2} + A C . A B$
View Solution
In any $Δ A B C$ , prove that
$a c cos B - b c cos A = (a^{2} - b^{2})$
View Solution
In a quadrilateral $A B C D$ prove that $A B^{2} + B C^{2} + C D^{2} + D A^{2} = A C^{2} + B D^{2} + 4 P Q^{2} w h e r e P a n d Q$ are middle points of diagonals $A C a n d B D .$
View Solution
In a quadrilateral $A B C D,$ prove that $A B^{2} + B C^{2} + C D^{2} + D A^{2} = A C^{2} + B D^{2} + 4 P Q^{2},$ where $P$ and $Q$ are middle points of diagonals $A C$ and $B D .$
View Solution
In $A B C, A B = A C,$ and the bisectors of angles $B$ and $C$ intersect at point $O$ . Prove that $B O = C O$ and the ray $A O$ is the bisector of angles $B A C .$
View Solution
In $Δ A B C, A B = A C$ and the bisectors of $∠ B and ∠ C$ meet at a point O. Prove that BO = CO and the ray AO is the bisector of $∠ A$ .

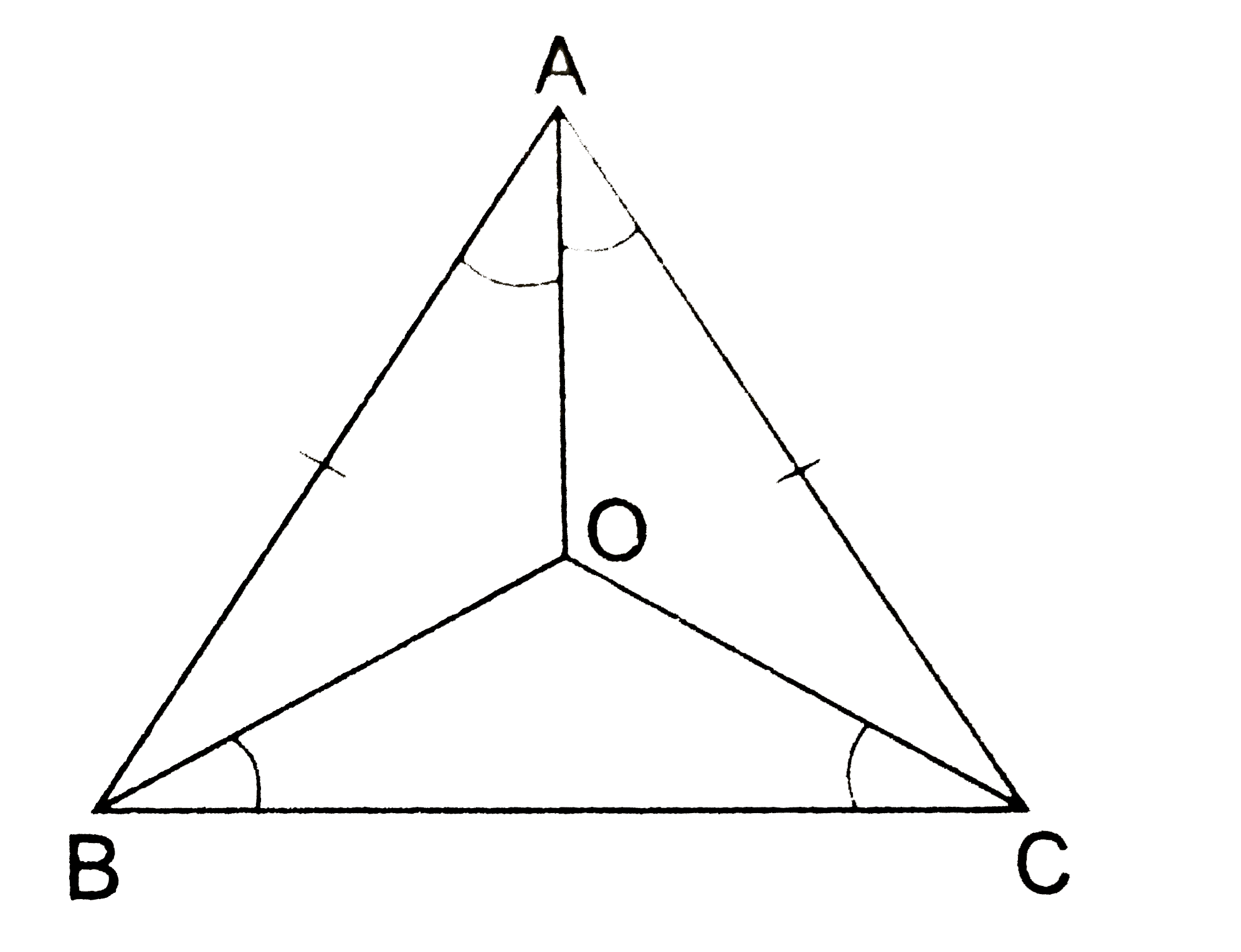
View Solution
$Δ A B C$ is isosceles with AC = BC . If $A B^{2} = 2 A C^{2}$ then find the measure of $∠ C$
View Solution
In $Δ A B C, A B = A C$ and the bisectors of $∠ B$ and $∠ C$ meet at a point $O$ . Prove that $B O = C O$ and the ray $A O$ is the bisector of $∠ A$ .
View Solution

In ΔABC prove that AB2+AC2=2(AO2+BO2); where O is the middle point of BC.

Similar Questions

Recommended Questions

In $Δ A B C$ prove that $A B^{2} + A C^{2} = 2 (A O^{2} + B O^{2})$ ; where O is the middle point of BC.