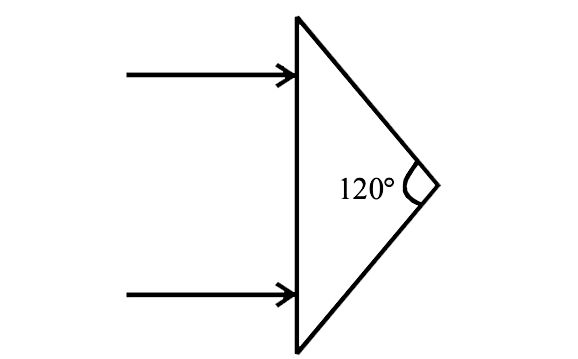
An isosceles prism of angle 120degree has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite faces
are parallel to each other
are diverging
make an angle 2sin−1(0.72) with each other
make an angle 2{sin−1(0.72)−30∘} with each other
The correct Answer is:D
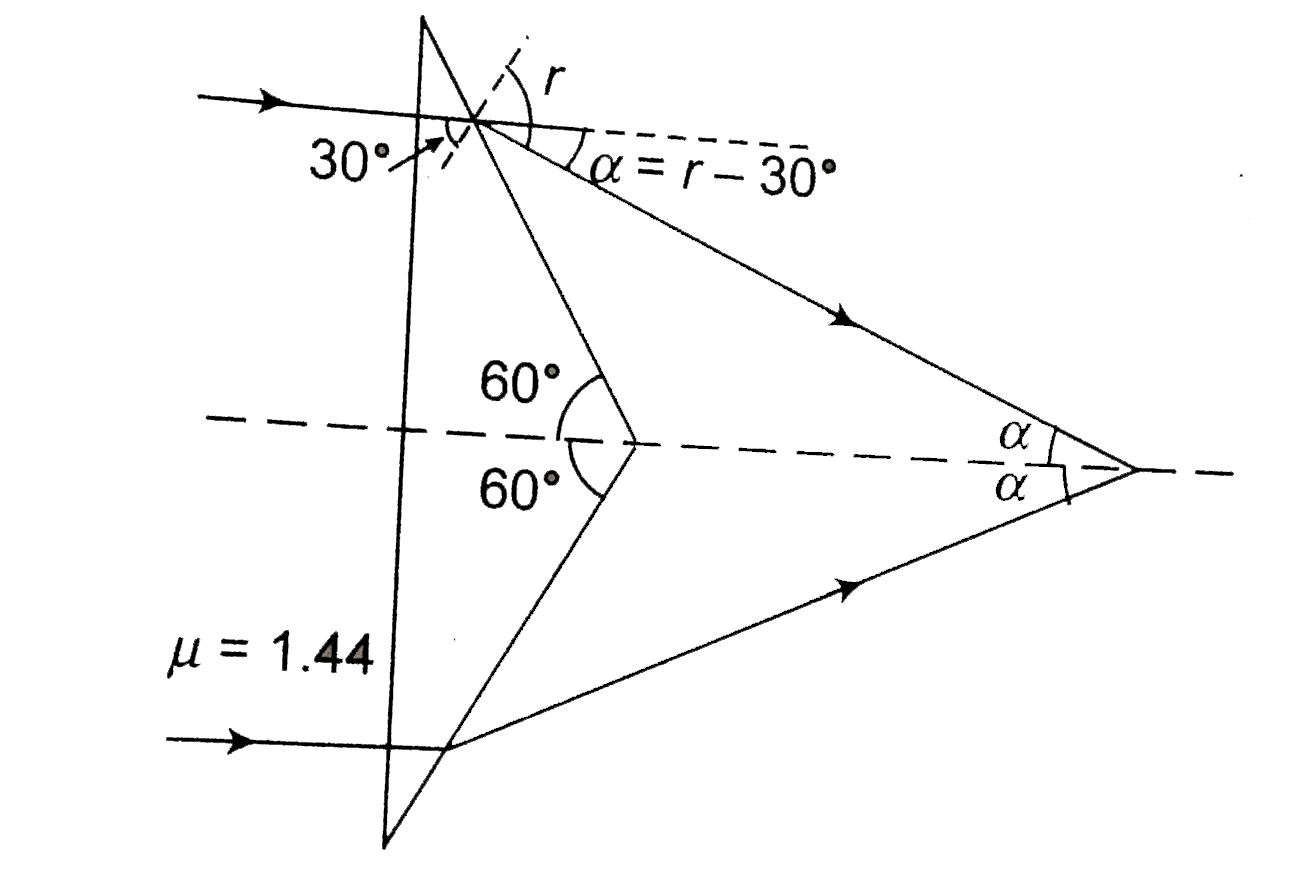
μsin30∘=1×sinr
1.44×12=sinr
r=sin−1(0.72)
Angle between emergent rays
=2α=2(r−30∘)
=2(sin−1(0.72)−30∘)
Topper's Solved these Questions
- BOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises110videos
REFRACTION OF LIGHT BY PLANE SURFACES
- BOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES105videos
REFRACTION AT SPHERICAL SURFACES
- BOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises140videos
SEMICONDUCTORS
Similar Questions
An isosceles prism has one of the refracting surfaces silvered. A ray of light is incident normally on the refracting face AB. After two reflections, the ray emerges from the base of the prism perpendicular to it. Find the angle of the prism.
View Solution(a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index n of the material of prism in terms of the angle A ray angle of minimum deviation δm
(b) A ray of light PQ enters an isosceles right angles prism ABC of refractive index 1.5 as shown in figure .
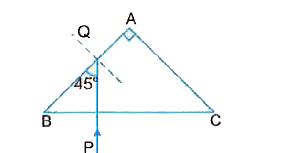
(i) Trace the path of the ray through the prism .
(ii) What will be the effect on the path of the ray if refractive index of the prism is 1.4 ?View Solution
Knowledge Check
- Question 1 - Select One
ABC is an isosceles right angled triangular reflecting prism of average refractive index μ . When incident rays on face AB are parallel to face BC , then they emerges from Face AC . which are also parallel to Face BC as shown in figure-l. The prism capable to do so , known as Dove Prism. In figure-ll, the Dove Prism is used for dispersion of incident light containing red colour and violet colour only. The red colour and violet colour lights are separated( displaced ) on screen by a distance Af. In reality , each ray of any colour has some width, which can be designated as d. It is clear that an observer can distinguish the red and violet rays that emerges from prism only if Δφ≥d .Otherwise the bundles of rays will overlap and mix.
Q Find the maximum value of width d of bundle of rays that can be resolved at the outlet of Dove Prism as shown in the figure-ll.
 A2.25×10−3mB2.25×10×−4mC1.125×10−3D1.125×10−4m
A2.25×10−3mB2.25×10×−4mC1.125×10−3D1.125×10−4m - Question 2 - Select One
The refractive index of the material of prism is 72 and Its refracting angle is 30°. One of the refracting surfaces of the prism is made a mirror in wards. A beam of monochromatic light enters the prism from the other surface and the ray retraces from the mirrored surface. The angle of incidence is
A30∘B45∘C60∘D0∘ - Question 3 - Select One
The path of a refracted ray of light in a prism is parallel to the base of the prism only when the
Alight of a particular wavelengthBray is incident normally at one faceCray under goes minimum deviationDnone of these
The refractive index of the material of a prism of refracting angle 45∘ is 1.6 for a certain monochromatic ray. What will be the minimum angle of incidence of this ray on the prism so that no TIR takes place as the ray comes out of the prism.
View SolutionThe prism shown in figure has a refractive index of 1.60 and the angles A are 30∘. Two light rays P and Q are parallel as they enter the prism. What is the angle between them after they emerge? [sin−1(0.8)=53∘]
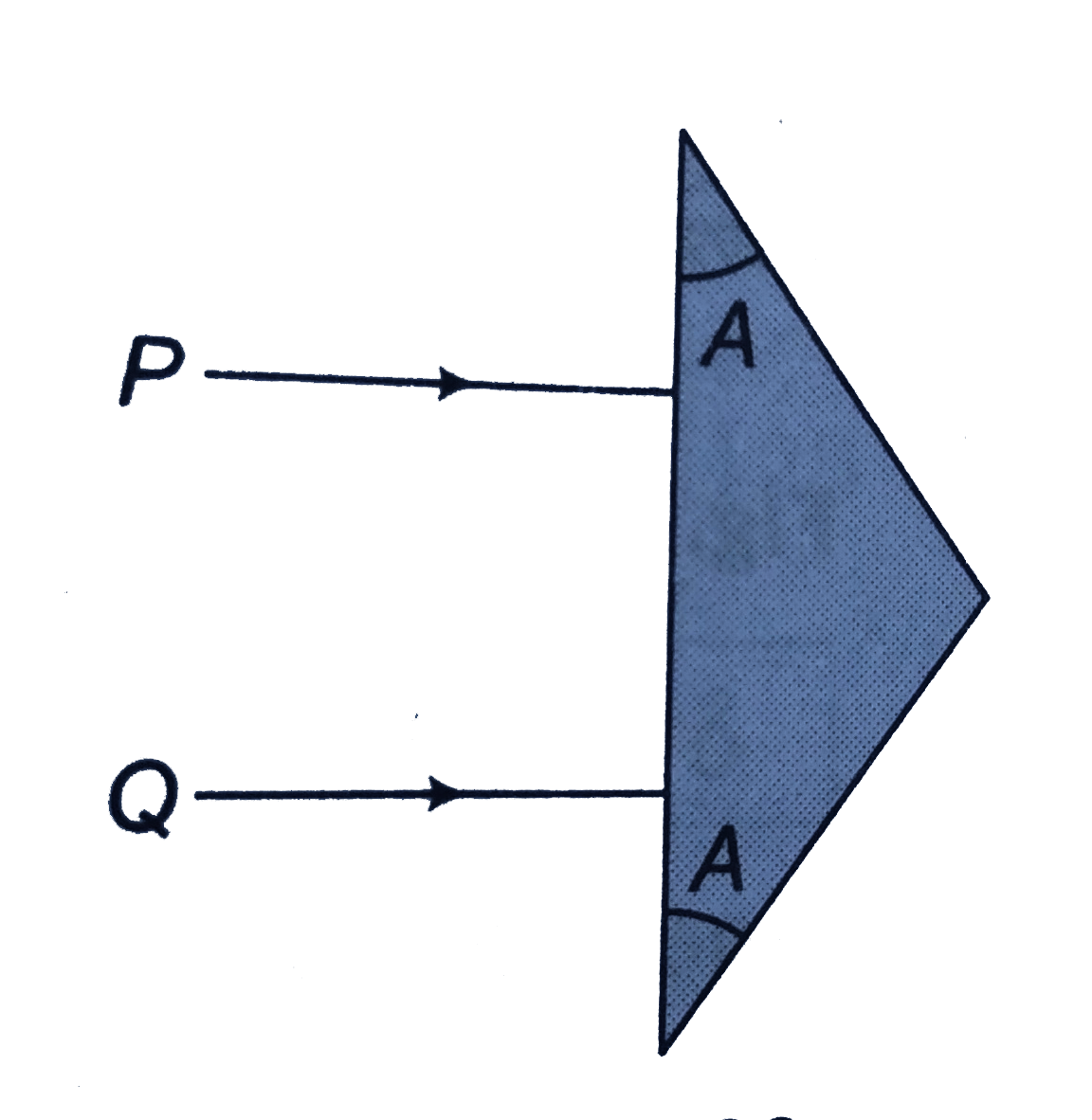 View Solution
View SolutionThe refractive index of the material of a prism of refracting angle 74∘ is 1.66 for a certain monochromatic ray. What should be the minimumangle of incidence of this ray on the prism so that no total internal reflection takes place as they come out of the prism.
View SolutionThe path of a refracted ray of light in a prism is parallel to the base of the prism only when the
View SolutionMonochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
 View Solution
View Solution

