In figure, the angle of inclination of the inclined plane is 30∘. Find the horizontal velocity V0 so that the particle hits the inclined plane perpendicularly.
 .
.
The correct Answer is:D
0=v0cos30∘−gsin30∘t⇒v0cos30∘gsin30∘...(1)
−Hcos30∘=−v0sin30∘t−12gcos30∘t2...(2)
By equation (1) and (2), we get
H=v20g[1+cot2α2]⇒v0=√2gH5=4m/s(α=30∘)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi single answer30videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi multiple answer16videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Passage15videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
In the given figure , the angle of inclination of the inclined plane is 30∘. A particle is projected with horizontal velocity v0 from height H. Find the horizotnal velocity v0 (in m/s) so that the particle hits the inclined plane perpendicu lar .Given H=4m, g=10m/s2.
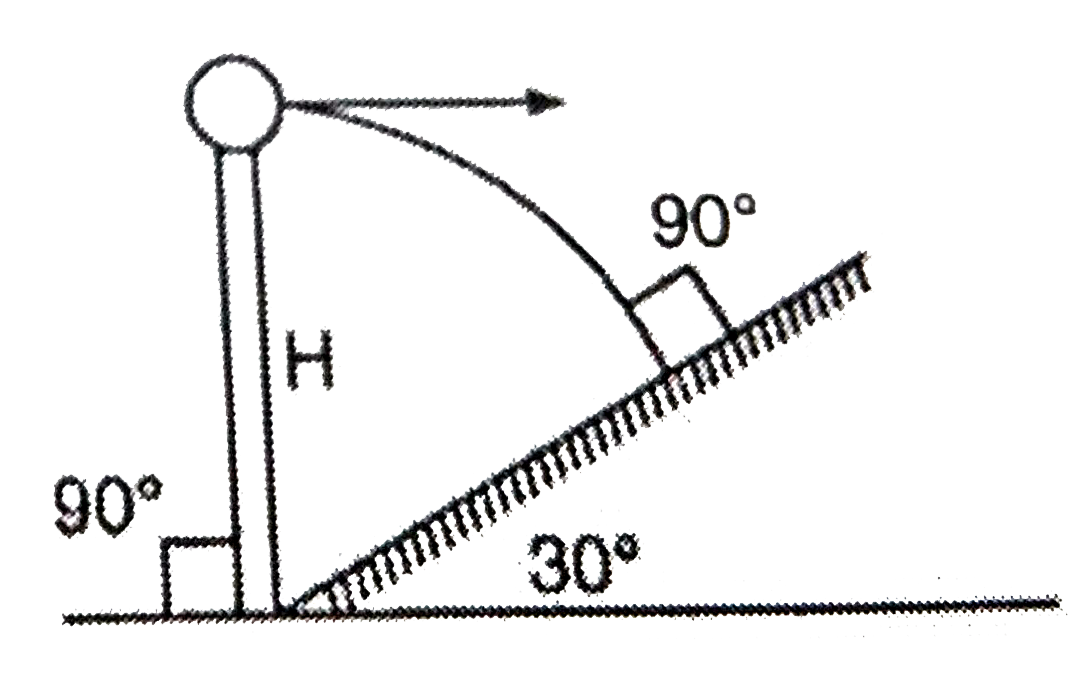 View Solution
View SolutionIn figure, find the horizontal velocity u(∈ms−1) of a projectile so that it hits the inclined plane perpendicularly. Given H=6.25m.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
By increasing the angle of inclination, the M.A. of an inclined plane
Adecreases.Bincreases.Cremains the same.Ddepends on the load to be raised. - Question 2 - Select One
If the angle of inclination of an inclined plane of 30∘, its mechanical advantage is ______
A30B43467C2DNone of the three - Question 3 - Select One
A particle is projected with a velocity of 20 m/s at an angle of 30∘ to an inclined plane of inclination 30∘ to the horizontal. The particle hits the inclined plane at an angle 30∘, during its journey. The time of flight is -
A4√3B2√3C√3D√32
A projectile is thrown at an angle θ with an inclined plane of inclination β as shown in fig. 1E108. Find the relation between β and θ ifv :
(a)projectile strikezs the inclined plane perpendicularly,
(b) projectile strikes the inclined plane horizontal.View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
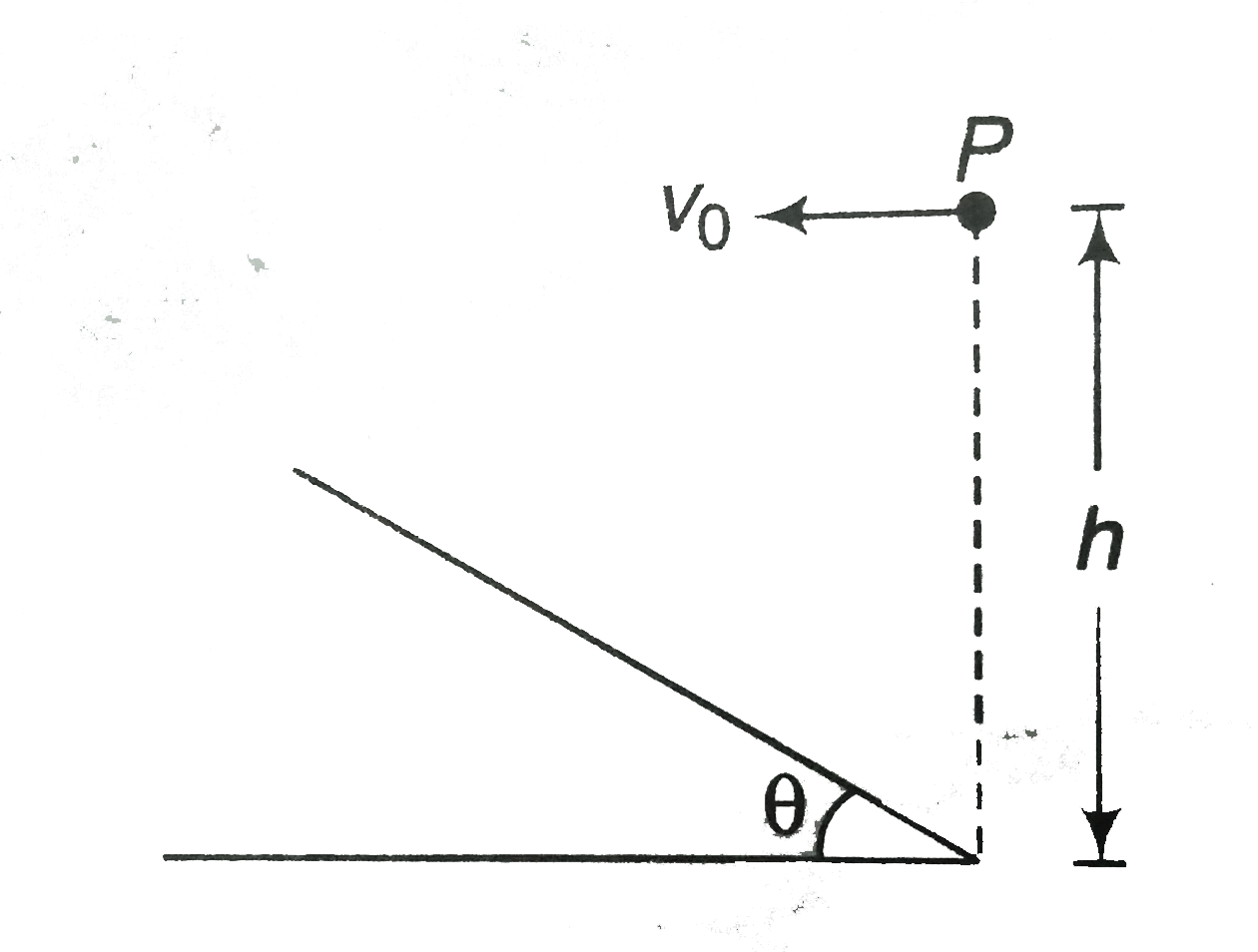 View Solution
View SolutionA particle is thrown horizontally from the top of an inclined plane , with a speed of 5m/s . If the inclination of the plane is 30∘ with the horizontal , how far from the point of projection will the particle strike the plane ?
View SolutionA particle is to be projected horizontally with velocity v from a point P, which is 60m above the foot of a plane inclined at angle 45∘ with horizontal as shown in figure. The particle hits the plane perpendicularly at A. After rebound from inlined plane it again hits at B. If coefficient of restitution between particles and plane is 1√2 then,
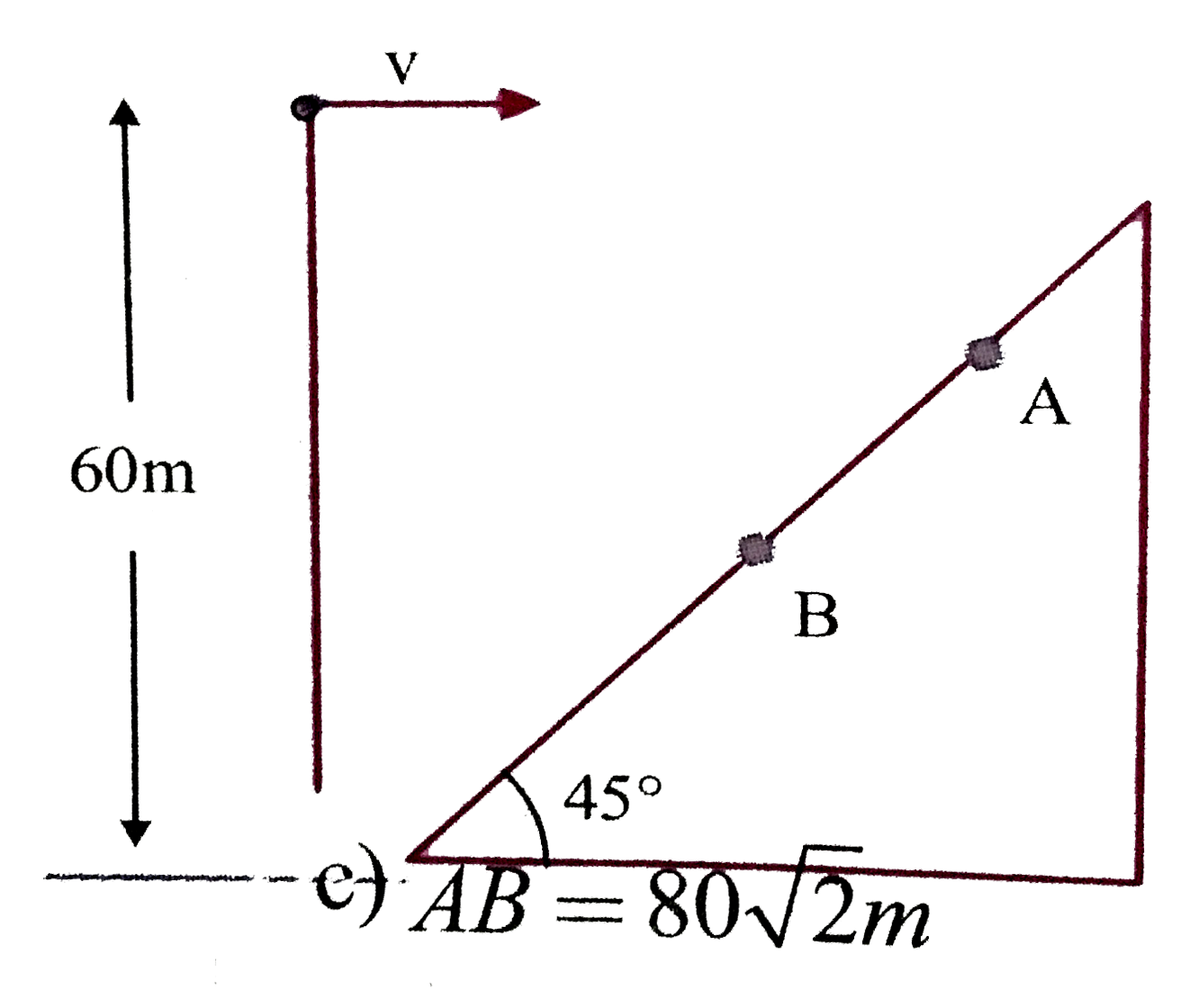 View Solution
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
 View Solution
View Solution

