In a given triangle ABC,DE∣∣BC and ADDB=35. If AC=5.6 , find AE .
To solve the problem step by step, we will use the properties of similar triangles and the given ratios.
1. Identify the Given Information:
- Triangle ABC
- Line segment DE is parallel to BC
- Ratio ADDB=35
- Length AC=5.6
- We need to find AE.
Hint: Write down all the given information clearly to avoid confusion later.
2. Use the Property of Similar Triangles:
- Since DE∥BC, by the Basic Proportionality Theorem (or Thales' theorem), triangles ADE and ABC are similar.
- This gives us the angle relationships:
- ∠ADE=∠ABC
- ∠AED=∠ACB
Hint: Remember that parallel lines create corresponding angles that are equal.
3. Set Up the Ratio of the Sides:
- From the similarity of triangles, we can write:
ADAB=AEAC
- Let AB=AD+DB. Since ADDB=35, we can express AD and DB in terms of a common variable:
- Let AD=3x and DB=5x.
- Therefore, AB=AD+DB=3x+5x=8x.
Hint: Use variables to simplify the ratios and make calculations easier.
4. Substitute the Ratios into the Similarity Equation:
- Substitute AD and AB into the similarity ratio:
ADAB=3x8x=38
- Thus, we have:
AEAC=38
Hint: Ensure you simplify the ratios correctly to maintain accuracy.
5. Substitute the Known Length:
- We know AC=5.6, so we can substitute this into the equation:
AE5.6=38
Hint: Always double-check the values you substitute into the equations.
6. Solve for AE:
- Cross-multiply to find AE:
AE=38×5.6
- Calculate AE:
AE=3×5.68=16.88=2.1
Hint: Break down the multiplication and division step-by-step to avoid mistakes.
Final Answer:
AE=2.1
- Triangle ABC
- Line segment DE is parallel to BC
- Ratio ADDB=35
- Length AC=5.6
- We need to find AE.
- Since DE∥BC, by the Basic Proportionality Theorem (or Thales' theorem), triangles ADE and ABC are similar.
- This gives us the angle relationships:
- ∠ADE=∠ABC
- ∠AED=∠ACB
- From the similarity of triangles, we can write:
ADAB=AEAC
- Let AB=AD+DB. Since ADDB=35, we can express AD and DB in terms of a common variable:
- Let AD=3x and DB=5x.
- Therefore, AB=AD+DB=3x+5x=8x.
- Substitute AD and AB into the similarity ratio:
ADAB=3x8x=38
- Thus, we have:
AEAC=38
- We know AC=5.6, so we can substitute this into the equation:
AE5.6=38
- Cross-multiply to find AE:
AE=38×5.6
- Calculate AE:
AE=3×5.68=16.88=2.1
AE=2.1
Topper's Solved these Questions
Similar Questions
In a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=6 cm , DB=9 cm and AE=8 cm , find AC . (ii) If ADDB=34 and AC=15 cm , find AE . (iii) If ADDB=23 and AC=18 cm , find AE .
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DEBC If AD=2 cm , AB=6 cm and AC=9 cm , find AE . (ii) If ADBD=45 and EC=2.5 cm , find AE . (iii) If AD=x , DB=x−2 , AE=x+2 and EC=x−1 , find the value of x .
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)= 2:5 (b) 4:25 (c) 4:15 (d) 8:125
View SolutionIn Fig. 4.178, DEBC (FIGURE) If DE=4cm , BC=6cm and Area (ADE)=16 cm2 , find the area of ABC . (ii) If DE=4cm, BC=8cm and Area (ADE)=25 cm2 , find the area of ABC . (iii) If DE:BC=3:5 . Calculate the ratio of the areas of ADE and the trapezium BCED .
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
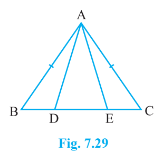
View SolutionFill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View Solution
