In Fig. 4.246, if PBCF and DPEF , then ADDE= (FIGURE) 34 (b) 13 (c) 14 (d) 23
Step by step video & image solution for In Fig. 4.246, if P B C F and D P E F , then (A D)/(D E)= (FIGURE) 3/4 (b) 1/3 (c) 1/4 (d) 2/3 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Fig. 4.246, if PBCF and DPEF , then ADDE= (FIGURE) 34 (b) 13 (c) 14 (d) 23
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionABJH, JDEF, ACEG are squares. BCAB=3 . Area BCDJArea HJFG=?
(a) 19
(b) 13
(c) 1
(d) 3
View SolutionIn Fig. 4.128, DEFG is a square and ∠BAC=90o . Prove that AGFDBG (ii) AGFEFC (FIGURE) (iii) DBGEFC (iv) DE2=BD×EC
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionIn Fig. 10.78, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then, (FIGURE) AD=AB+BC+CA (b) 2AD=AB+BC+CA (c) 3AD=AB+BC+CA (d) 4AD=AB+BC+CA
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)= 2:5 (b) 4:25 (c) 4:15 (d) 8:125
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
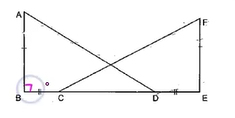
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
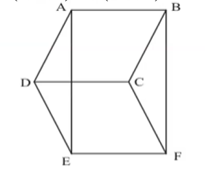
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
View Solution
