In Figure, PQRS is a parallelogram. If XandY
are mid-points of PQandSR
respectively and diagonal SQ
is jointed. The ratio ar(| |(gm)XQRY):ar(QSR)=
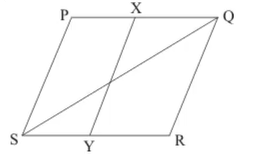
(a) 1:4
(b) 2:1
(c) 1:2
(d) 1:1
Step by step video & image solution for In Figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SR respectively and diagonal SQ is jointed. The ratio ar (|\ |(gm) XQRY): ar (QSR)= (a) 1:4 (b) 2:1 (c) 1:2(d) 1:1 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, PQRS is a parallelogram. If XandY are mid-points of PQandSR respectively and diagonal SQ is jointed. The ratio ar(| |(gm)XQRY):ar(QSR)=

(a) 1:4
(b) 2:1
(c) 1:2
(d) 1:1
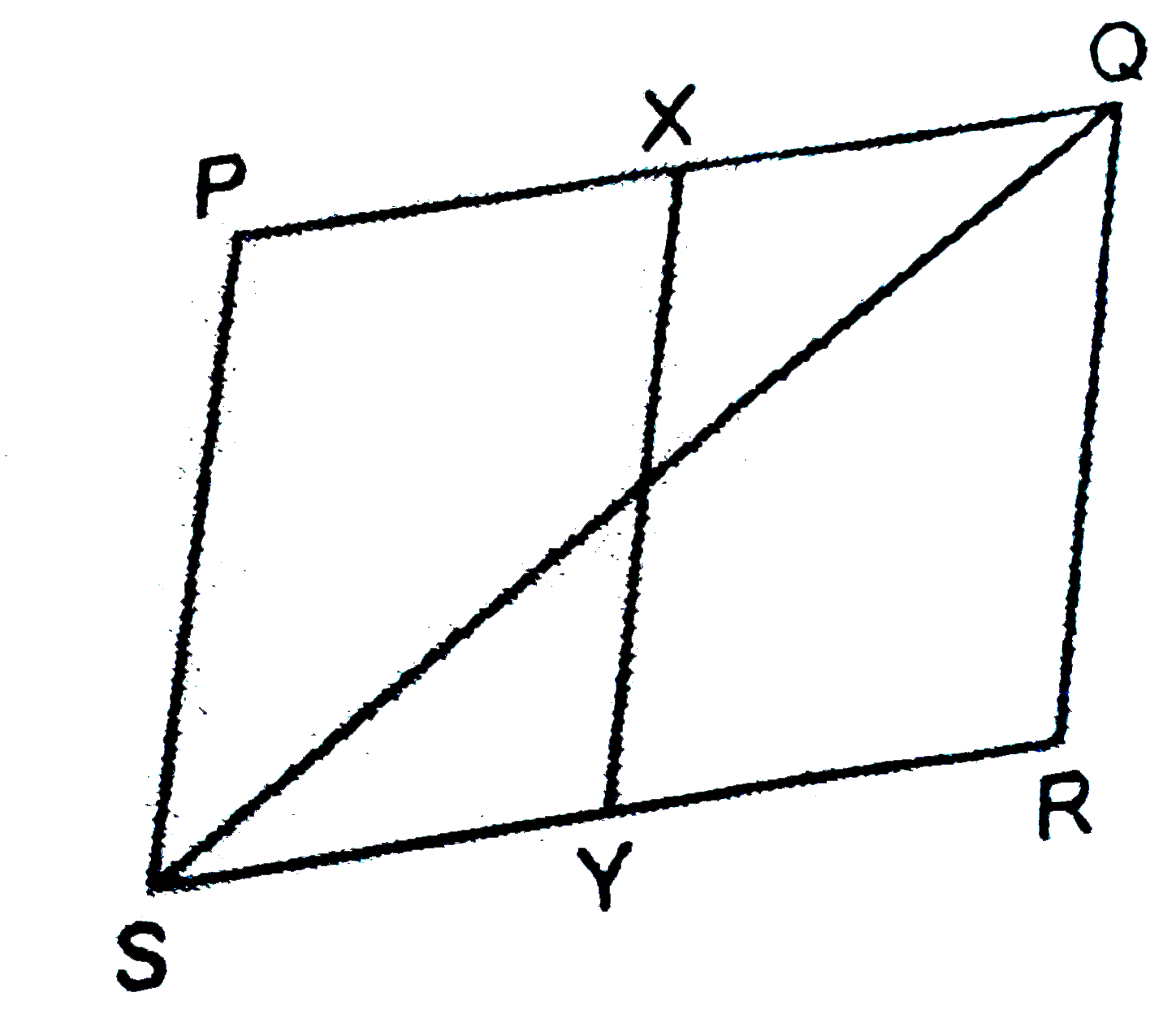
View SolutionIn the given figure, PQRS is a parallelogram. If X and Y are mid-point of PQ and SR respectively and diagonal SQ is joined. Find the ratio of area of (∣∣gmXQRY): area (ΔQSR)
View Solution
Knowledge Check
If in parallelogram ABDC, the coordinate of A, B and C are respectively (1,2), (3,4) and (2,5), then the equation of the diagonal AD is
A3x+5y−13=0B3x−5y+7=0C5x−3y+1=0D5x+3y−11=0
□PQRS is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
AB+AC=12(PR+SQ).
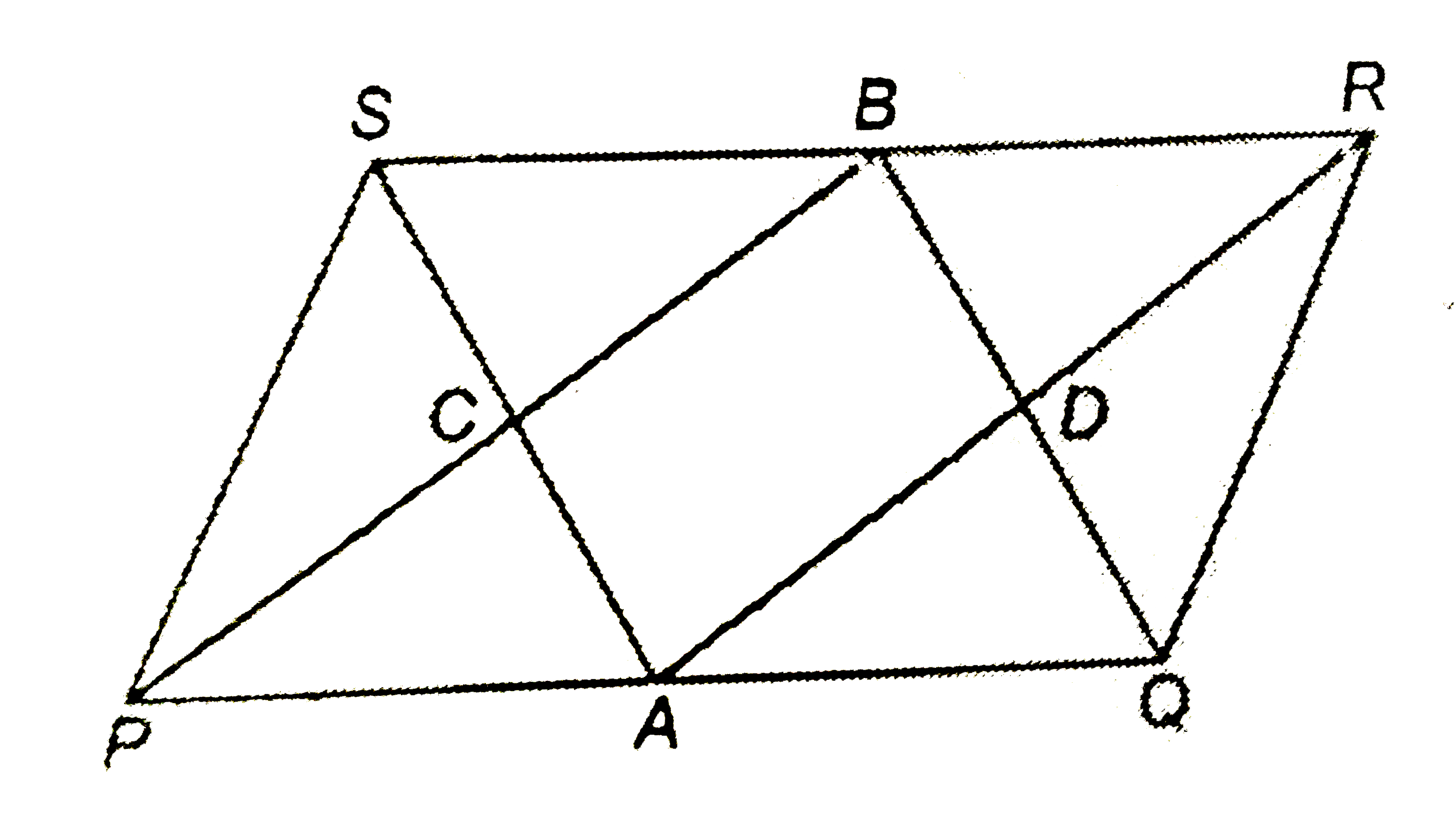
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
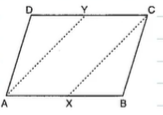
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
View SolutionABCD is a rectangle and E and F are the mid-points of AD and DC respectively. Then the ratio of the areas of EDF and AEFC would be (a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 2 : 3
View SolutionShow that the line joining any vertex of a parallelogram to the mid - point of an opposite side divides the opposite diagonal in the ratio 2 : 1.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionA straight line through the origin o meets the parallel lines 4x+2y=9 and 2x+y+6=0 points P and Q respectively. Then the point o divides the segment PQ in the ratio: : (A) 1:2 (B) 3:2 (C) 2:1 D) 4:3
View Solution