Thirty women were examined in a hospital by a doctor and the number of heart beats per minute recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method. No. of heat 65-68 68-71 71-74 74-77 77-80 80-83 83-86 beats (per min.) No. of women: 2 4 3 8 7 4 2
To find the mean heart beats per minute for the 30 women based on the given data, we will follow these steps:
Step 1: Create a Frequency Table
We will first list the class intervals and their corresponding frequencies.
| Class Interval (beats/min) | Frequency (f) |
|----------------------------|---------------|
| 65 - 68 | 2 |
| 68 - 71 | 4 |
| 71 - 74 | 3 |
| 74 - 77 | 8 |
| 77 - 80 | 7 |
| 80 - 83 | 4 |
| 83 - 86 | 2 |
| Total | 30 |
Step 2: Calculate the Midpoint (x_i) for Each Class Interval
The midpoint for each class interval is calculated as follows:
xi=Lower limit+Upper limit2
| Class Interval (beats/min) | Frequency (f) | Midpoint (x_i) |
|----------------------------|---------------|-----------------|
| 65 - 68 | 2 | 66.5 |
| 68 - 71 | 4 | 69.5 |
| 71 - 74 | 3 | 72.5 |
| 74 - 77 | 8 | 75.5 |
| 77 - 80 | 7 | 78.5 |
| 80 - 83 | 4 | 81.5 |
| 83 - 86 | 2 | 84.5 |
Step 3: Choose an Assumed Mean (a)
We can choose the midpoint of the central class interval as the assumed mean. Here, the central class interval is 74 - 77, and its midpoint is:
a=75.5
Step 4: Calculate the Deviation (d_i)
The deviation di is calculated as:
di=xi−a
| Midpoint (x_i) | Deviation (d_i) |
|-----------------|------------------|
| 66.5 | 66.5 - 75.5 = -9 |
| 69.5 | 69.5 - 75.5 = -6 |
| 72.5 | 72.5 - 75.5 = -3 |
| 75.5 | 75.5 - 75.5 = 0 |
| 78.5 | 78.5 - 75.5 = 3 |
| 81.5 | 81.5 - 75.5 = 6 |
| 84.5 | 84.5 - 75.5 = 9 |
Step 5: Calculate fi⋅di
Now, we will calculate the product of frequency and deviation for each class interval.
| Frequency (f) | Deviation (d_i) | fi⋅di |
|----------------|------------------|----------------------|
| 2 | -9 | -18 |
| 4 | -6 | -24 |
| 3 | -3 | -9 |
| 8 | 0 | 0 |
| 7 | 3 | 21 |
| 4 | 6 | 24 |
| 2 | 9 | 18 |
Step 6: Calculate the Summation of Frequencies and fi⋅di
Now, we sum the frequency and fi⋅di:
- Σfi=30
- Σ(fi⋅di)=−18−24−9+0+21+24+18=12
Step 7: Calculate the Mean
Using the formula for the mean:
Mean=a+Σ(fi⋅di)Σfi
Substituting the values:
Mean=75.5+1230
Mean=75.5+0.4
Mean=75.9
Final Answer
The mean heart beats per minute for these women is 75.9 beats/min.
---
We will first list the class intervals and their corresponding frequencies.
|----------------------------|---------------|
| 65 - 68 | 2 |
| 68 - 71 | 4 |
| 71 - 74 | 3 |
| 74 - 77 | 8 |
| 77 - 80 | 7 |
| 80 - 83 | 4 |
| 83 - 86 | 2 |
| Total | 30 |
The midpoint for each class interval is calculated as follows:
xi=Lower limit+Upper limit2
|----------------------------|---------------|-----------------|
| 65 - 68 | 2 | 66.5 |
| 68 - 71 | 4 | 69.5 |
| 71 - 74 | 3 | 72.5 |
| 74 - 77 | 8 | 75.5 |
| 77 - 80 | 7 | 78.5 |
| 80 - 83 | 4 | 81.5 |
| 83 - 86 | 2 | 84.5 |
We can choose the midpoint of the central class interval as the assumed mean. Here, the central class interval is 74 - 77, and its midpoint is:
a=75.5
The deviation di is calculated as:
di=xi−a
|-----------------|------------------|
| 66.5 | 66.5 - 75.5 = -9 |
| 69.5 | 69.5 - 75.5 = -6 |
| 72.5 | 72.5 - 75.5 = -3 |
| 75.5 | 75.5 - 75.5 = 0 |
| 78.5 | 78.5 - 75.5 = 3 |
| 81.5 | 81.5 - 75.5 = 6 |
| 84.5 | 84.5 - 75.5 = 9 |
Now, we will calculate the product of frequency and deviation for each class interval.
|----------------|------------------|----------------------|
| 2 | -9 | -18 |
| 4 | -6 | -24 |
| 3 | -3 | -9 |
| 8 | 0 | 0 |
| 7 | 3 | 21 |
| 4 | 6 | 24 |
| 2 | 9 | 18 |
Now, we sum the frequency and fi⋅di:
- Σ(fi⋅di)=−18−24−9+0+21+24+18=12
Using the formula for the mean:
Mean=a+Σ(fi⋅di)Σfi
Mean=75.5+1230
Mean=75.5+0.4
Mean=75.9
The mean heart beats per minute for these women is 75.9 beats/min.
Topper's Solved these Questions
Similar Questions
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method.
View SolutionThirty women were examined in a hospital by a doctor and the number of heat beats per minute were recorded and summarised as follows:
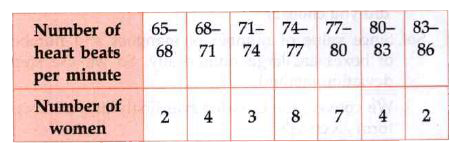 Find number of women have heart bean lessthan 80 and more than 71
Find number of women have heart bean lessthan 80 and more than 71
View Solution
Knowledge Check
In the following question, select the related letters from the given alternatives.
AGN : IOV : : BLM : ?A(a) JTUB(b) KTUC(c) JUVD(d) TUJ
The number of students absent in a class were recorded every day for 120 days and the information is given in the following frequency table: No. of students absent (x) : 0 1 2 3 4 5 6 7 No. of days (f) : 1 4 10 50 34 15 4 2 Find the mean number of students absent per day.
View SolutionStudents of a class were tested to find their pulse rate. The following figures were obtained for the number of beats per minute.
70, 60, 70, 68, 67, 62, 71, 71, 59, 73, 73, 60, 60, 62, 6, 68, 70, 70, 74, 69
How many students are there whose pulse rate is more than 60 per minute ?
View SolutionThe following table production yield in kg per hectare of wheat of 150 farms in a village . Culculate the mean , median and mode of the production yeild.
Production Yield (kg per hectare)50−5353−5656−5959−6262−6565−6868−7171−7474−77Number of Farms 3 8 14 30 36 28 16 10 5
View SolutionStudy the following information carefully and answer the given questions :
A word and number arrangement machine when given an input line of words and numbers rearranges them following a particular rule in each step. The following is an illustration of rearrangement
Input :day 74 night 36 25 68 all for
Step I : all day 74 night 36 25 68 84
Step II : all 74 day night 36 25 68
Step III : all 74 day 68 night 36 25 for
Step IV : all 74 day 68 for night 36 35
Step V : all 74 day 68 for 36 night 25
and Step V is the last step of the rearrangement of the above input
As per the rules followed in the above steps, find out in the following questions the appropriate step for the given input.
Step III of an Input : bond 86 goal 12 33 like high 46
Which of the following will be step VII ?
1) bond 86 goal 46 like 12 33 high
2) bond 86 goal 46 high like 33 12
3) bond 86 goal 46 high 33 like 12
4) There will be no such step
5) None of these
View SolutionStudy the following information carefully and answer the given questions :
A word and number arrangement machine when given an input line of words and numbers rearranges them following a particular rule in each step. The following is an illustration of rearrangement
Input :day 74 night 36 25 68 all for
Step I : all day 74 night 36 25 68 84
Step II : all 74 day night 36 25 68
Step III : all 74 day 68 night 36 25 for
Step IV : all 74 day 68 for night 36 35
Step V : all 74 day 68 for 36 night 25
and Step V is the last step of the rearrangement of the above input
As per the rules followed in the above steps, find out in the following questions the appropriate step for the given input.
Step II of an Input : car 73 18 25 wear 49 long
Which of the following is definitely the input ?
1) 18 25 wear 49 long for car 73
2) 73 18 car wear 49 long for
3) 18 73 25 car wear 49 long for
4) Cannot be determined
5) None of these
View SolutionStudy the following information carefully and answer the given questions :
A word and number arrangement machine when given an input line of words and numbers rearranges them following a particular rule in each step. The following is an illustration of rearrangement
Input :day 74 night 36 25 68 all for
Step I : all day 74 night 36 25 68 84
Step II : all 74 day night 36 25 68
Step III : all 74 day 68 night 36 25 for
Step IV : all 74 day 68 for night 36 35
Step V : all 74 day 68 for 36 night 25
and Step V is the last step of the rearrangement of the above input
As per the rules followed in the above steps, find out in the following questions the appropriate step for the given input.
Step IV of an Input : dear 63 few 51 16 29 yrs now
How many more steps will be required to complete the arrangement ?
1) Four
2) Five
3) Three
4) Two
5) None of these
View SolutionStudy the following information carefully and answer the given questions :
A word and number arrangement machine when given an input line of words and numbers rearranges them following a particular rule in each step. The following is an illustration of rearrangement
Input :day 74 night 36 25 68 all for
Step I : all day 74 night 36 25 68 84
Step II : all 74 day night 36 25 68
Step III : all 74 day 68 night 36 25 for
Step IV : all 74 day 68 for night 36 35
Step V : all 74 day 68 for 36 night 25
and Step V is the last step of the rearrangement of the above input
As per the rules followed in the above steps, find out in the following questions the appropriate step for the given input.
Input : war 52 and peace 43 16 now 24
How many steps will be required to complete the rearrangement ?
1) Four
2) Five
3) Six
4) Seven
5) None of these
View Solution
