The following table shows the marks scored by 140 students in an examination of a certain paper:
{Marks0−1010−2020−3030−4040−50No. of students2024403620
Calculate the average marks by using all the three methods: direct method, assumed mean deviation and shortcut method.
To calculate the average marks scored by 140 students using three different methods: the Direct Method, the Assumed Mean Method, and the Shortcut Method, we will follow the steps outlined below.
Given Data
| Marks | No. of Students |
|-----------|------------------|
| 0 - 10 | 20 |
| 10 - 20 | 24 |
| 20 - 30 | 40 |
| 30 - 40 | 36 |
| 40 - 50 | 20 |
Step 1: Direct Method
1. Calculate Mid-values (x_i):
- For each class interval, the mid-value is calculated as:
- xi=Lower Limit+Upper Limit2
- Mid-values:
- For 0-10: x1=0+102=5
- For 10-20: x2=10+202=15
- For 20-30: x3=20+302=25
- For 30-40: x4=30+402=35
- For 40-50: x5=40+502=45
2. Create a Table with Mid-values and Calculate f_i x_i:
| Marks | No. of Students (f_i) | Mid-value (x_i) | f_i x_i |
|-----------|------------------------|------------------|---------|
| 0 - 10 | 20 | 5 | 100 |
| 10 - 20 | 24 | 15 | 360 |
| 20 - 30 | 40 | 25 | 1000 |
| 30 - 40 | 36 | 35 | 1260 |
| 40 - 50 | 20 | 45 | 900 |
| Total | 140 | | 3620|
3. Calculate Mean:
- Mean ¯x=∑fixi∑fi=3620140=25.857
Step 2: Assumed Mean Method
1. Assume Mean (A):
- Let's assume A=25.
2. Calculate Deviation (u_i):
- ui=xi−A
- Deviations:
- For 0-10: u1=5−25=−20
- For 10-20: u2=15−25=−10
- For 20-30: u3=25−25=0
- For 30-40: u4=35−25=10
- For 40-50: u5=45−25=20
3. Create a Table with Deviations and Calculate f_i u_i:
| Marks | No. of Students (f_i) | u_i | f_i u_i |
|-----------|------------------------|------|---------|
| 0 - 10 | 20 | -20 | -400 |
| 10 - 20 | 24 | -10 | -240 |
| 20 - 30 | 40 | 0 | 0 |
| 30 - 40 | 36 | 10 | 360 |
| 40 - 50 | 20 | 20 | 400 |
| Total | 140 | | -120|
4. Calculate Mean:
- Mean ¯x=A+∑fiui∑fi=25+−120140=25−0.857=25.857
Step 3: Shortcut Method
1. Use the same mid-values and deviations as in the Assumed Mean Method.
2. Calculate the mean using the formula:
- Mean ¯x=A+h⋅∑fiui∑fi
- Where h=10 (width of the class interval).
- Mean ¯x=25+10⋅−120140=25−0.857=25.857
Final Result
- The average marks calculated using all three methods is 25.857.
| Marks | No. of Students |
|-----------|------------------|
| 0 - 10 | 20 |
| 10 - 20 | 24 |
| 20 - 30 | 40 |
| 30 - 40 | 36 |
| 40 - 50 | 20 |
- For each class interval, the mid-value is calculated as:
- xi=Lower Limit+Upper Limit2
- Mid-values:
- For 0-10: x1=0+102=5
- For 10-20: x2=10+202=15
- For 20-30: x3=20+302=25
- For 30-40: x4=30+402=35
- For 40-50: x5=40+502=45
| Marks | No. of Students (f_i) | Mid-value (x_i) | f_i x_i |
|-----------|------------------------|------------------|---------|
| 0 - 10 | 20 | 5 | 100 |
| 10 - 20 | 24 | 15 | 360 |
| 20 - 30 | 40 | 25 | 1000 |
| 30 - 40 | 36 | 35 | 1260 |
| 40 - 50 | 20 | 45 | 900 |
| Total | 140 | | 3620|
- Mean ¯x=∑fixi∑fi=3620140=25.857
- Let's assume A=25.
- ui=xi−A
- Deviations:
- For 0-10: u1=5−25=−20
- For 10-20: u2=15−25=−10
- For 20-30: u3=25−25=0
- For 30-40: u4=35−25=10
- For 40-50: u5=45−25=20
| Marks | No. of Students (f_i) | u_i | f_i u_i |
|-----------|------------------------|------|---------|
| 0 - 10 | 20 | -20 | -400 |
| 10 - 20 | 24 | -10 | -240 |
| 20 - 30 | 40 | 0 | 0 |
| 30 - 40 | 36 | 10 | 360 |
| 40 - 50 | 20 | 20 | 400 |
| Total | 140 | | -120|
- Mean ¯x=A+∑fiui∑fi=25+−120140=25−0.857=25.857
- Mean ¯x=A+h⋅∑fiui∑fi
- Where h=10 (width of the class interval).
- Mean ¯x=25+10⋅−120140=25−0.857=25.857
- The average marks calculated using all three methods is 25.857.
Topper's Solved these Questions
Similar Questions
The following table shows marks secured by the students of a class in an examination in English:
Marks0−1010−2020−3030−4040−50Number of Students 20 24 40 36 20
Calculte mean marks using Short-cut Method.
View SolutionThe following table shows marks secured by the students of a class in an examination in English:
Marks0−1010−2020−3030−4040−50Number of Students 20 24 40 36 20
Calculte mean marks using Short-cut Method.
View Solution
Knowledge Check
Given data shows marks of 32 students in an examination. Mean of the marks will be
Class interval0−1010−2020−3030−4040−50Frequency126842A18.125B21.875C22.425D22.545
The following table shows marks obtained by the students of a class in their test in English:
Marks0−1010−2020−3030−4040−50Number of Students 20 24 40 36 20
Calculate arithmetic mean using Step-deviation method.
View SolutionThe following table shows marks obtained by the students of a class in their test in English:
Marks0−1010−2020−3030−4040−50Number of Students 20 24 40 36 20
Calculate arithmetic mean using Step-deviation method.
View SolutionThe following table gives the marks scored by 100 students in an entrance examination.

View SolutionCalculate the mean devation from the mean the following data:
Marks0−1010−2020−3030−4040−50No. of stu.5815166
View SolutionThe following distribution table shows the marks scored by 140 students in an examination :
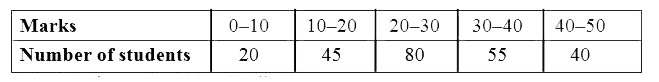
Calculate the mode of the distribution.
View SolutionFind out median marks from the following data :
Marks0−1010−2020−3030−4040−50Number of Students 8 30 40 12 10
View SolutionFollowing are the marks obtained by 30 students in a examination

Taking class intervals 0−10,10−20,…..40−50 construct a frequency table.
View Solution