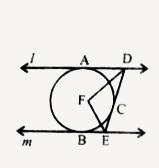
In fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between l and m. Find ∠DFE.
45∘
110∘
90∘
20∘
The correct Answer is:C
Step by step video & image solution for In fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between l and m. Find angle DFE. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Fig. 10.32, l and m are two parallel tangents at A and B . The tangent at C makes an intercept DE between l and m . Prove that ∠DFE=90o .
View SolutionIn the following figure, If l and m are two tangents and AB is a chord making and angle of 60∘ with the tangent l, then the angle between l and m is __________.

View Solution
Knowledge Check
In a circle, PQ and RS are two parallel tangents at A and B. The tangent at makes an intercept DE between PQ and RS. Then ∠DOE is equal to : (where O is centre).
A90∘B120∘C60∘D45∘PQ and RS are two parallel tangents to a circle with centre O and another tangent AB wih point of contact C intersect PQ at A and RS at B. then find ∠AOB
A60∘B120∘C90∘D180∘
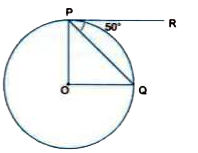
In Fig , O is the centre of a circle , PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ. Find ∠POQ .
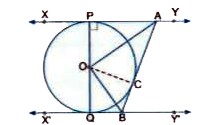
View SolutionIn Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
View Solutionlandm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
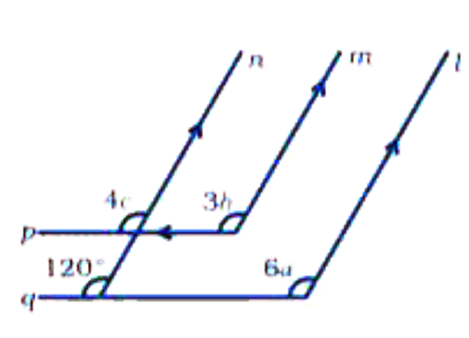
View SolutionIn Fig. 5.61, l, m and n are parallel lines, and the lines p and q are also parallel. Find the values of a, b and c.
View SolutionXYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View SolutionFind the distance between two parallel tangents of a circle of radius 3 cm.
View Solution
