AB
is a line segment. AX and BY
are two equal line
segments drawn on opposite sides of line AB
such that AX∣∣BY.
If AB and XY
intersect each other at
P,prove that
APX≅BPY
(ii) AB and XY
bisect each other.
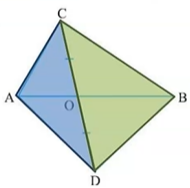
In the given figure, segment AXandBY are equa
In the given figure, segment AXandBY are equal
AX∣∣BY,The line segment AX∣∣BY and line segment AB join the parallel line at A and B.
And line segment XY cut line AB at point P.
Then, in △AXPand△PYB
AX=BY..(Given)
∠XAP(3)=∠YBP(4)(Adjacent∠)
∠AXP(1)=∠PYB(2)(Adjacent∠)
Then△APX≅△BPY
△APX≅△BPY,ThenAP=BPandXP=PY
Thus, the line segment AB and XY bisect each other.
Topper's Solved these Questions
Similar Questions
AB is a line segment, AX and BY are two equal line segments drawn on opposite sides of line AB such that AXBY. If AB and XY intersect each other P, prove that APX≅BPY AB and XY bisect each other.
View SolutionAB is a line segment, AX and BY are two equal line segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P, prove that
ΔAPX≅ΔBPYView SolutionAB is a line segment. AX and BY are two equal line segments drawn on opposite sides of line AB such that AX∣∣BY. If AB and XY intersect each other at P,prove that APX≅BPY (ii) AB and XY bisect each other.
In the given figure, segment AXandBY are equaView Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
 View Solution
View SolutionABCD is a parallelogram and line segments AX,CY bisect the angles AandC, respectively. Show that AX∣∣CY
View SolutionProve that the line xa+yb=1andxb−ya=1 are perpendicular to each other.
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionABCD is a trapezium with AB∣∣DC . A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View Solution

