AD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
Given, AD⊥AB
BC⊥AB
AD=BC
To Prove, CD,bisectsABorOA=OB
We can show that the two triangles OBC and OAD are congruent by using AAS congruency rule
then we can say corresponding parts of congruent triangles will be equal.
ADandBCare equal perpendiculars to a line segment AB(figure).
Show that, CD bisects AB.
Consider two △s \BOC and AOD\,/_BOC=/_AOD<br>/_CBO=/_DAO \Each\ 90^@<br>sinceAD \and\ BC are _|_ AB)<br>BC = AD(Given)<br>/_\BOC~=/_\AOD(∀S≅ruencere–)<br>BO = AO (By CPCT)
Thus,CD bisects AB and O is the mid-point of AB.
Topper's Solved these Questions
Similar Questions
In Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
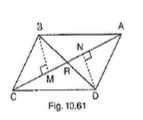View SolutionBD is one of the diagonals of a quadrilateral ABCD. AM and CN are the perpendiculars from A and C , respectively, on BD. Show That ar (qua..ABCD)=12BD.AM+CN
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionStatement 1: →a,→b,and→c are three mutually perpendicular unit vectors and →d is a vector such that →a,→b,→cand→d are non-coplanar. If [→d→b→c]=[→d→a→b]=[→d→c→a]=1,then→d=→a+→b+→c Statement 2: [→d→b→c]=[→d→a→b]=[→d→c→a]⇒→d is equally inclined to →a,→b,→c.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionStudy the diagram. The line l is perpendicular to line m (a) Is CE=EG (b) Does PE bisect CG = (c) Identify any two line segments for which PE is the perpendicular bisector. (d) Are these true? (i) AC>EG (ii) CD=GH (iii) BC<EH
View SolutionA quadrilateral ABCD is such that diagonal BD divides its area in two equal parts. Prove that BD bisects AC. GIVEN : A quadrilateral ABCD in which diagonal BD bisects it. i.e. ar(ABD)=ar(BDC) CONSTRUCTION : Join AC Suppose AC and BD intersect at O . Draw AL⊥BD and CMBD. TO PROVE : AO=OC.
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
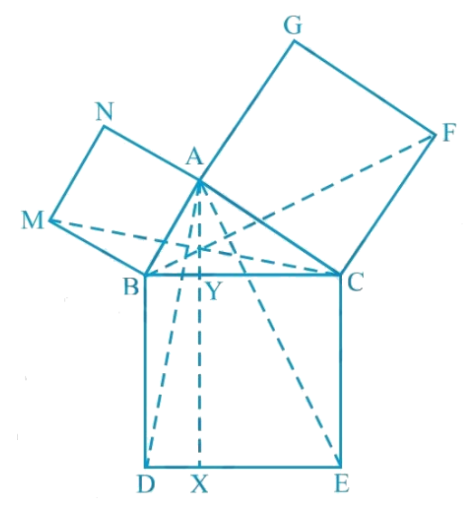View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
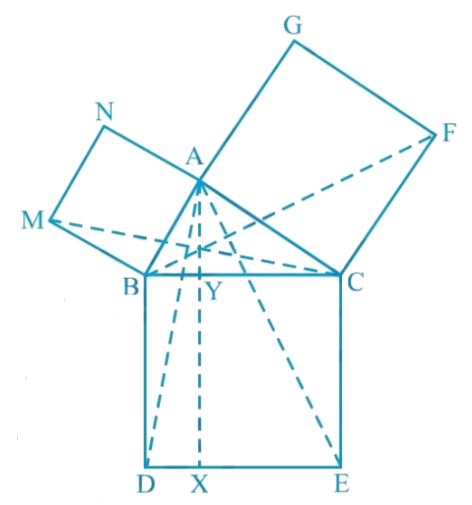View Solution