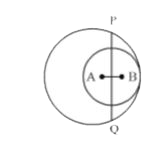
In Figure,
two circles with centres A and B
and of
radii 5 cm and 3 cm
touch each other internally. If the perpendicular bisector of segment AB
meets the
bigger circle in P and Q
, find the
length of PQ
Aand B are the centres of the circles with radii 5cm and 3cm respectively.
C is the mid-point of AB.
Extend AB upto O point on circumference of outer circle.
AB=AO−BO=5−3=2cm (since AO and BO are radii of larger and smaller circles)
AC=AB2=22=1cm
now in right angled triangle AMP,AC=1cm,AP=5cm
by pythagoras therom , AP2=PC2+AC2
PC2=√AP2−AC2
PC2=√52−12
Therefore,PQ=2PC=2√24
=4√6cm(CP=CQ)
To solve the problem step by step, we will follow the reasoning provided in the video transcript and derive the length of segment PQ.
1. Identify the Radii and Centers:
- Let the radius of the larger circle (center A) be rA=5cm.
- Let the radius of the smaller circle (center B) be rB=3cm.
2. Find the Distance Between the Centers (AB):
- Since the circles touch each other internally, the distance AB can be calculated as:
AB=rA−rB=5cm−3cm=2cm
3. Determine the Midpoint C of Segment AB:
- The midpoint C of segment AB can be calculated as:
AC=AB2=2cm2=1cm
4. Apply the Pythagorean Theorem in Triangle APC:
- In right triangle APC, where AP is the radius of the larger circle, we have:
- AP=5cm
- AC=1cm
- According to the Pythagorean theorem:
AP2=PC2+AC2
- Substituting the known values:
52=PC2+12
25=PC2+1
5. Solve for PC:
- Rearranging the equation gives:
PC2=25−1=24
- Taking the square root:
PC=√24=2√6cm
6. Calculate the Length of PQ:
- Since PQ is twice the length of PC (because C is the midpoint of PQ):
PQ=2×PC=2×2√6=4√6cm
Final Answer:
The length of segment PQ is 4√6cm.
---
- Let the radius of the larger circle (center A) be rA=5cm.
- Let the radius of the smaller circle (center B) be rB=3cm.
- Since the circles touch each other internally, the distance AB can be calculated as:
AB=rA−rB=5cm−3cm=2cm
- The midpoint C of segment AB can be calculated as:
AC=AB2=2cm2=1cm
- In right triangle APC, where AP is the radius of the larger circle, we have:
- AP=5cm
- AC=1cm
- According to the Pythagorean theorem:
AP2=PC2+AC2
- Substituting the known values:
52=PC2+12
25=PC2+1
- Rearranging the equation gives:
PC2=25−1=24
- Taking the square root:
PC=√24=2√6cm
- Since PQ is twice the length of PC (because C is the midpoint of PQ):
PQ=2×PC=2×2√6=4√6cm
The length of segment PQ is 4√6cm.
Topper's Solved these Questions
Similar Questions
In Figure, two circles with centres A and B and of radii 5 cm and 3 cm touch each other internally. If the perpendicular bisector of segment AB meets the bigger circle in P and Q , find the length of PQ
Aand B are the centres of the circles with radii 5cm and 3cm respectively.
C is the mid-point of AB.
Extend AB upto O point on circumference of outer circle.
AB=AO−BO=5−3=2cm (since AO and BO are radii of larger and smaller circles)
AC=AB2=22=1cm
now in right angled triangle AMP,AC=1cm,AP=5cm
by pythagoras therom , AP2=PC2+AC2
PC2=√AP2−AC2
PC2=√52−12
Therefore,PQ=2PC=2√24
=4√6cm(CP=CQ)View SolutionIn the figure, two circles with centres AandB and of radii 5cmand3cm touch each other intermally. If the perpendicular bisectors of segment AB meets the bigger circle in PandQ. Find the length of PQ.
View Solution
Knowledge Check
- Question 1 - Select One
Two circles whose centres are A & B touches internally to each other as shown in figure their radii are 5 and 3 units respectively. The perpendicular bisector of AB meets at P and Q on the outer circle. Find the length of PQ.
 A4√6B4C2√6D2
A4√6B4C2√6D2 - Question 2 - Select One
A and B are centres of the two circles whose radii are 5 cm and 2 cm respectively. The direct common tangents to the circles meet AB extended at P.Then p divides AB
Ainternally in the ratio 5:2Binternally in the ratio 2:5Cexternally in the ratio 5:2Dexternally in the ratio 7:2 - Question 3 - Select One
Three circles with centres A, B and C and with unit radii touch each other at O, P and Q. Find the area of the shaded region .
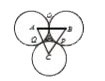 A0.16 sq. unitsB1.21 sq. unitsC0.03 sq. unitsD0.32 units
A0.16 sq. unitsB1.21 sq. unitsC0.03 sq. unitsD0.32 units
In the adjoining figure, two circle with centres at A and B, and of radii 5 cm and 3 cm touch each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.
View SolutionDraw circles with centres A,B and C each of radius 3 cm, such that each circle touches the other two circles.
View SolutionTwo circles having radii 3.5 cm and 4.8 cm touch each other internally. Find the distance between thir centres.
View SolutionTwo concentric circles are of radii 5cm and 3cm respectively. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo circles with radii 5 cm and 4.5 cm touch each other externally then find the distance between their centre.
View Solution

