If Figure, AOC is a diameter of the circle and are AXB=12 arc BYC. Find ∠BOC
As arcAXB=12arcBYC
∠AOB=12∠B0C
∠AOB+∠BOC=1800
12∠B0C+∠BOC=1800
∠BOC=23×1800=1200
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
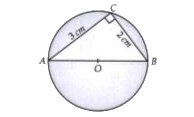
In the given figure (not to scale ) , O is the centre of the circle . A ,B,C and D are conyclic and AB =CD . If ∠MON=120∘ , then find ∠OPN .
 A20∘B30∘C40∘D60∘
A20∘B30∘C40∘D60∘
A circle intersects an ellipse x2a2+y2b2=1 precisely at three points A,B,C as shown in the figure. AB is a diameter of the circle and isperpendicular to the major axis of the ellipse. If the eccentricity ofthe ellipse is 45, find the length of the diameter AB in terms of a.
View SolutionIn Fig. 15.69, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm , find the area of the shaded region. (FIGURE)
View SolutionPQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR=120o , then ∠OPQ is 60o (b) 45o (c) 30o (d) 90o
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).
 View Solution
View SolutionIn Figure, O and O' are centres of two circles intersecting at B and C.ACD is a straight line, find x
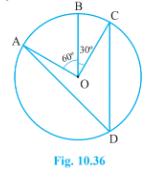
View SolutionIn Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC= 30o and ∠AOB= 60o. If D is a point on the circle other than the arc ABC, find ∠ADC.
 View Solution
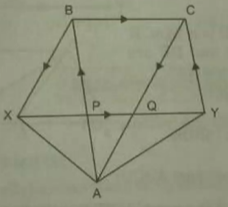
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
 View Solution
View Solution