Find the acceleration of each block in the situation shown in the figure. All the surface are smooth and the pulleys and sttings are light.

Video Solution
Text Solution
In this problem, two blocks are moving with different acceleration because they travel different distances in same time. If blocks travel different distances in same time. Their accelerations are proportional to distance travelled.
Considwer the motion of pulley B, if it goes down by a distance x0, the block of mass 2m will also move by x0 but the block of mass m will move by 2x0. If an acceleration of 2m is a, the acceleration of m will be 2a
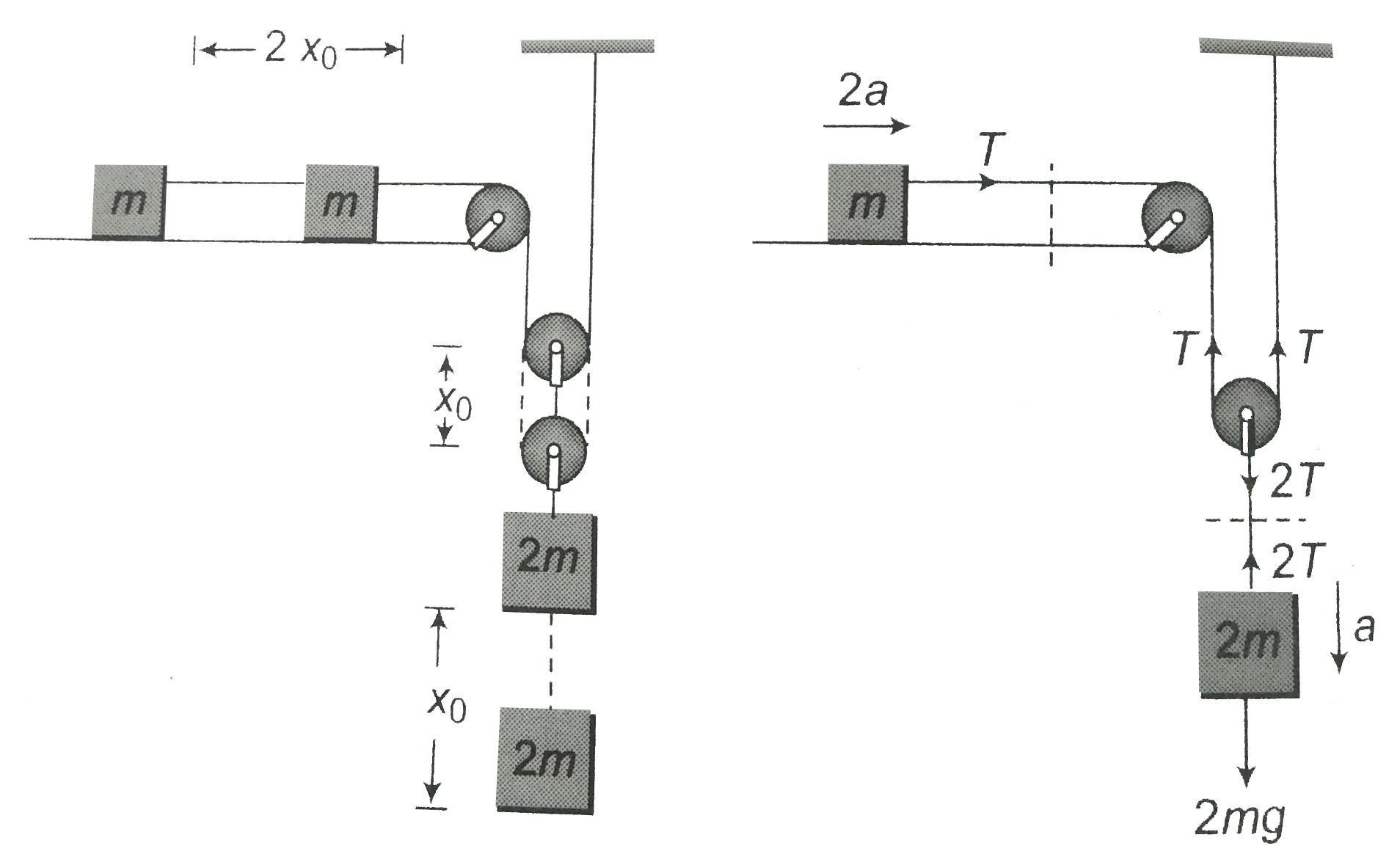
2m:↓:2mg−2T=2ma (i)
m→:T=m×2a (ii)
From (i) and (ii)
2mg−4ma=2ma⇒6ma=2mg⇒a=g3
Acceleration of 2m:g3
m:2g3
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider the situation shown in figure. All the surface are smooth. The tension in the string connected to 2m is.
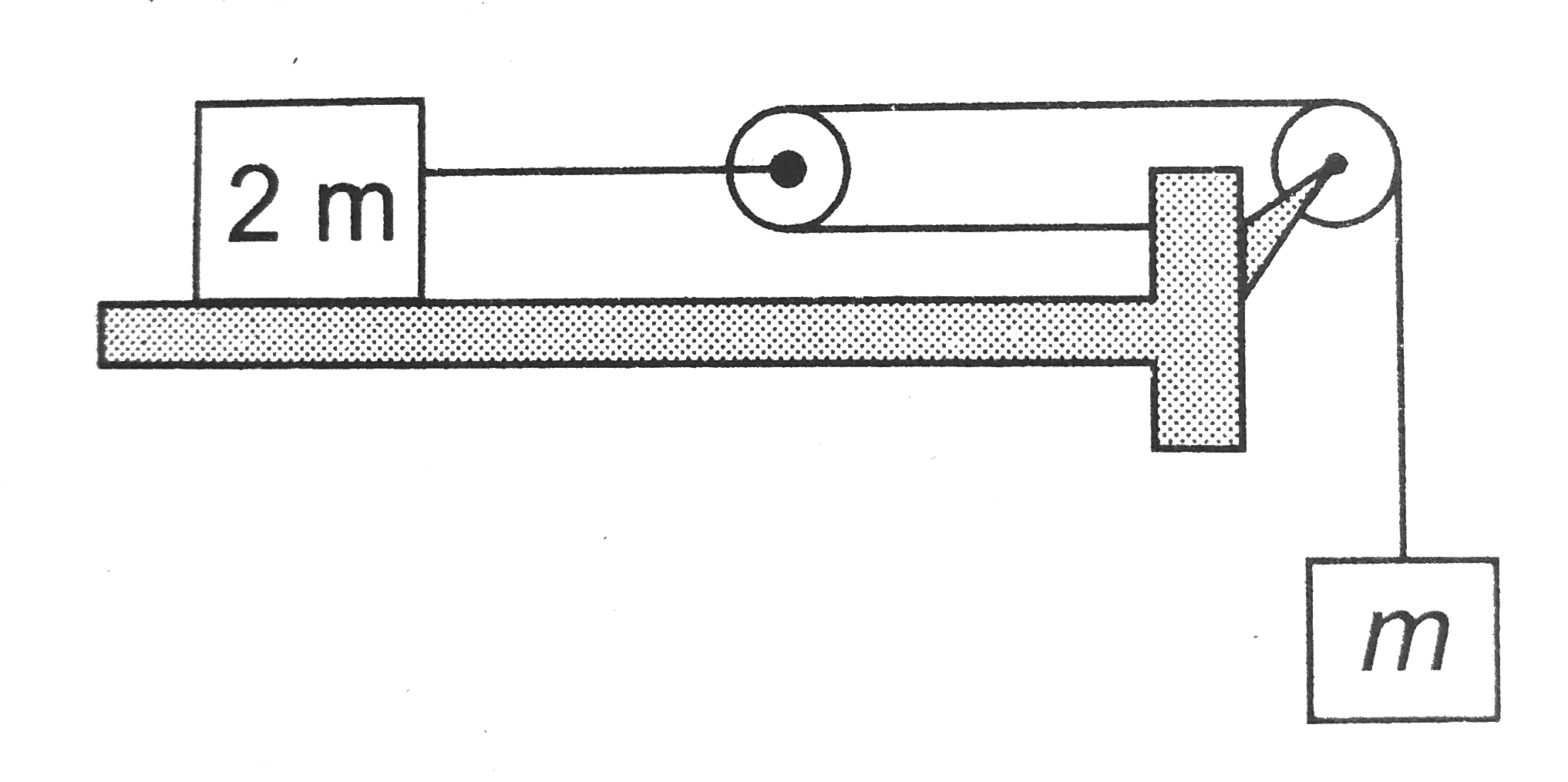 Amg3B4mg3C2mg3Dmg
Amg3B4mg3C2mg3DmgFind the acceleration of the 6 kg block in the figure. All the surfaces and pulleys are smooth. Also the strings are inextensible and light. [Take g=10m/s2]
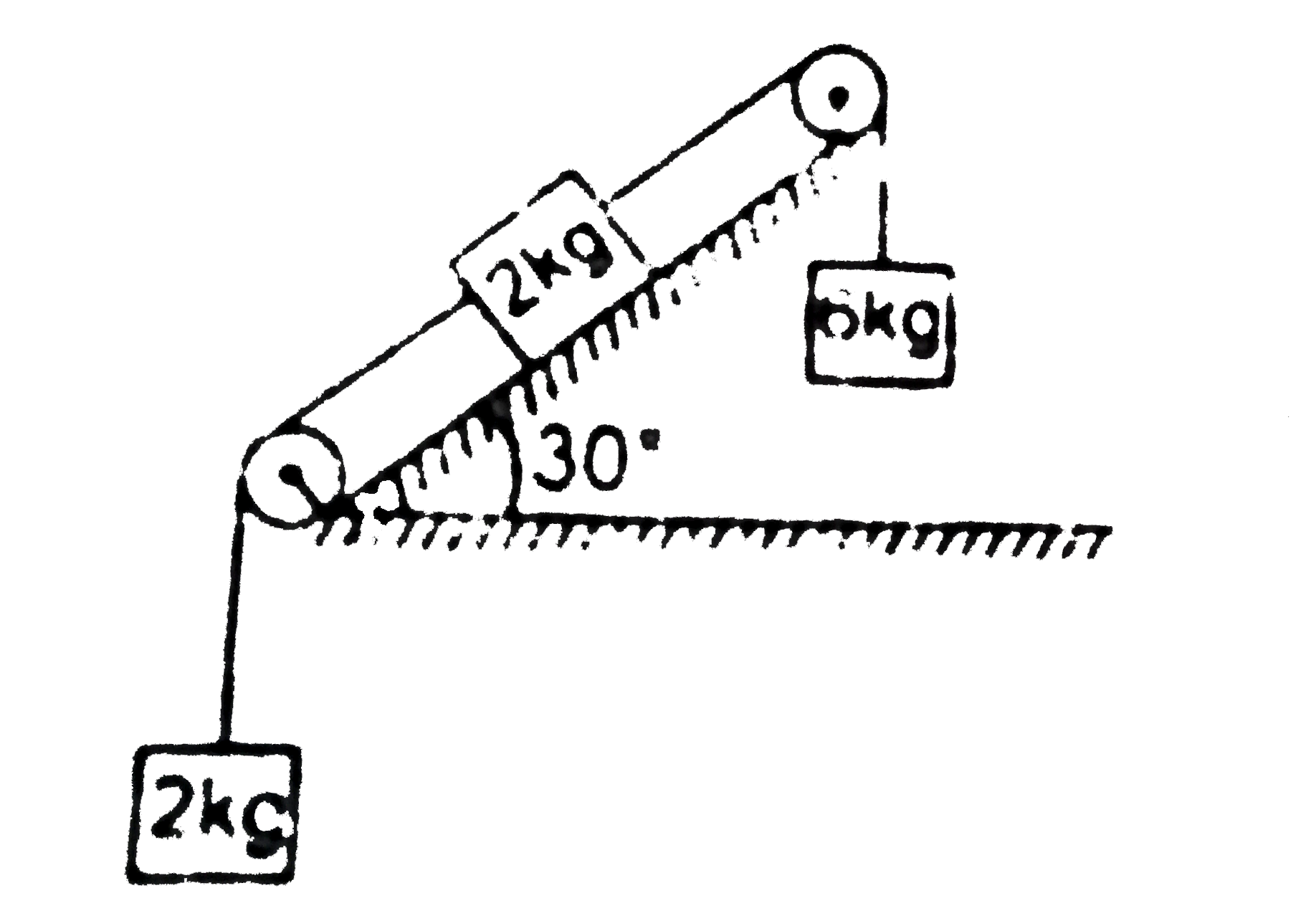 .A3m/s2B4m/s2C5m/s2D2m/s2
.A3m/s2B4m/s2C5m/s2D2m/s2The acceleration of small block m with respect to ground is (all the surface are smooth):
AgBg/2CZeroD√2g
Find the acceleration of the blocks A and B in the three situations shown in figure.

View SolutionIn the diagram shown in figure ,all pulleys are smooth and massless and stings are light . Match the following

View SolutionConsider the situation as shown in the figure. All the surface are smooth and the string and pulley are light. Find the mass of the hanging block which will prevent the smaller block form slipping over the triangular block.

View SolutionThe acceleration of the block (A) and (B) respectively in situation shown in the figure is: (pulleys and string are massless).
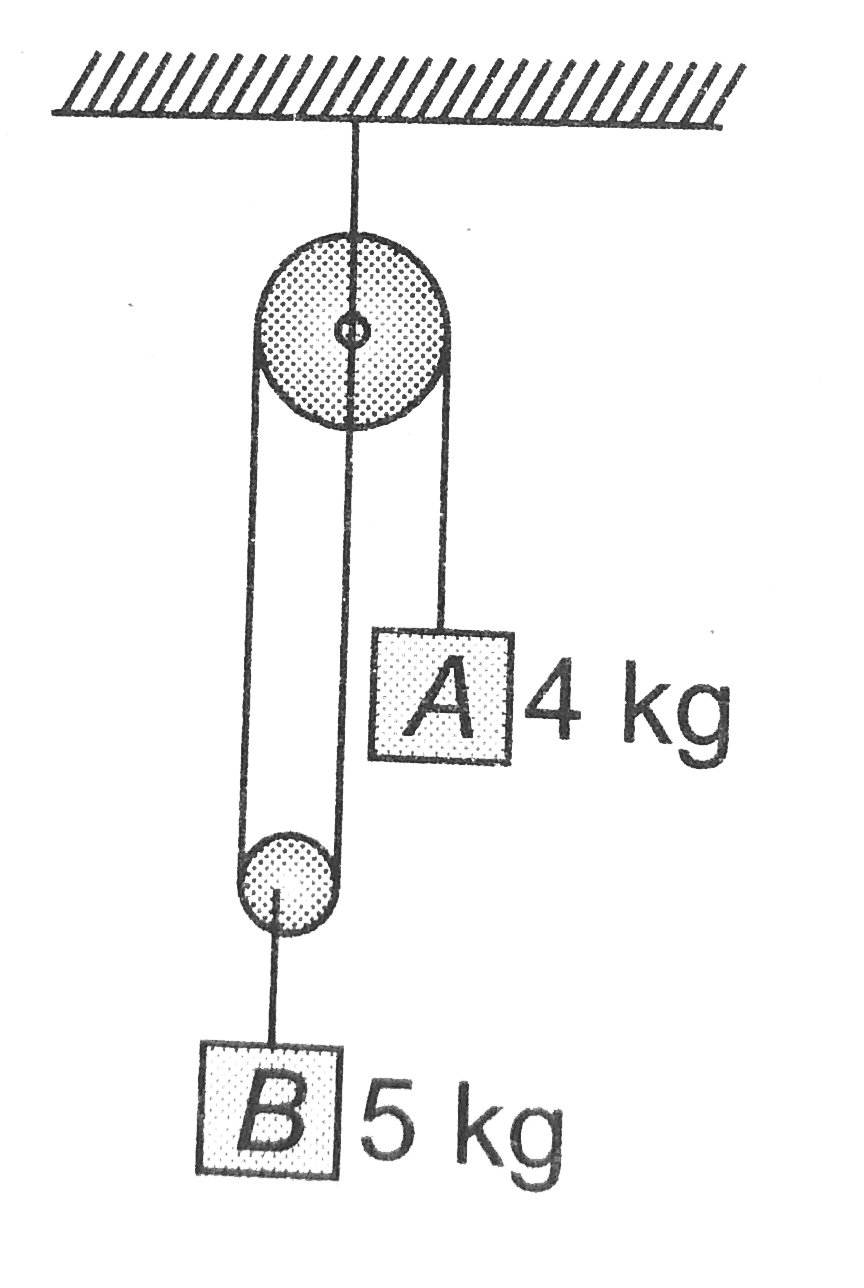
View SolutionConsider the situation shown in the figure. The wall is smooth but the surfaces of A and B in contact are rough. Then,
View Solution

