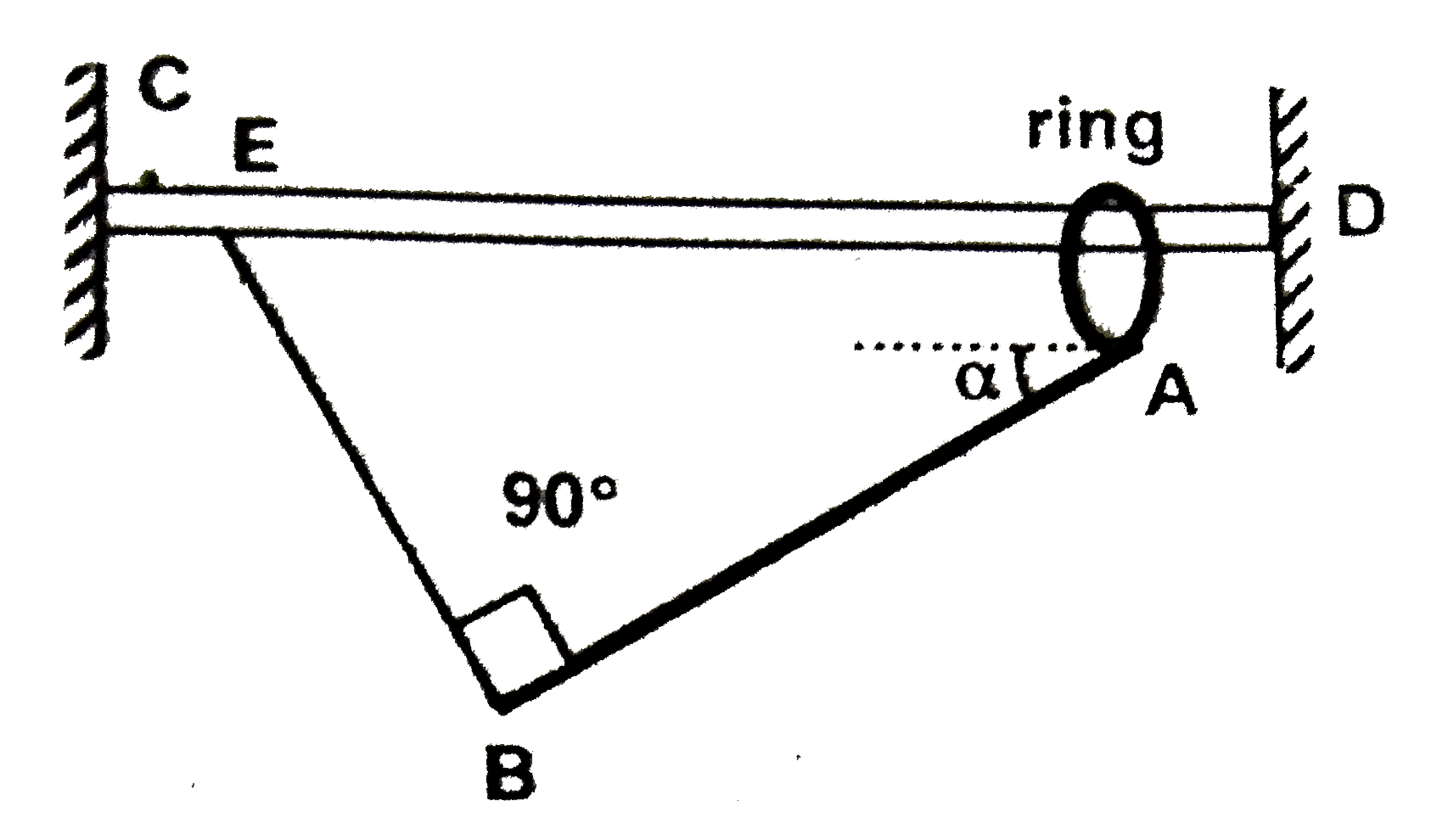
One end of a heavy uniform rod AB can slide along rough horizontal guiding surface CD with the help of massless ring as shown in the figure. The dimension of ring is negligible. BE is the ideal string if ∠EBA is right angle and α is the angle between rod AB and horizontal when the rod is on the verge of sliding. Find the coefficient of friction between ring and horizontal guiding surface CD.
tanα2+tan2α
tanα1+2tan2α
tanα2−tanα
tanα1−tan2α
The correct Answer is:B

Since body is in equilibrium under the influence of three forces only so they must e concurrent. Using Lami's theorem we can write
tanα=L2x and tan(α+λ)=Lx
tan(α+λ)=2tanα⇒tanα+tanλ1−tanαtanλ=2tanα
⇒tanα+tanλ=2tanα−2tan2αtanλ
⇒tanλ=μ=tanα1+2tan2α
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions

One-fourth length of a uniform rod of mass m and length l is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is μ.
View Solution
One-fourth length of a uniform rod of mass m and length l is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is μ.
View Solution
Knowledge Check
The end of a heavy uniform rod AB can slide along a rough horizontal rod AC to which it is attached by a ring. B and C are joined by a string. If ABC be a right angle, when the rod is on the point of sliding, μ the coefficient of friction and α the angle between AB and the vertical, then
Aμ=2tanα/(2+tan2α)Bμ=tanα/(2+tan2α)Cμ=2cotα/(1+cot2α)Dμ=cotα/(2+cot2α)A uniform ring placed on a rough horizontal surface is given a sharp impulse as shown in the figure-5.130. As a consequence, it acquires a linear velocity of 2m/s. If coefficient of friction between the ring and the horizontal surface is 0.4 :
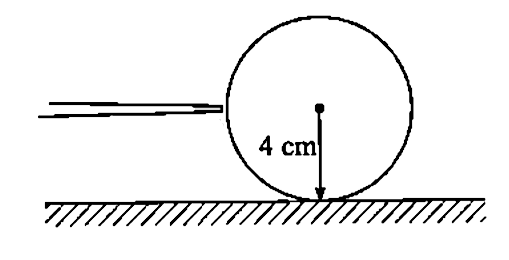 ARing wil lstart pure rolling afler O.25sBWhen ring will start pure rolling its .velocity is 1m//sCAfter 0.5s from impulse its velocity is 1m//s.DAfter0.125 s from impulse its velocity is 1m//s.
ARing wil lstart pure rolling afler O.25sBWhen ring will start pure rolling its .velocity is 1m//sCAfter 0.5s from impulse its velocity is 1m//s.DAfter0.125 s from impulse its velocity is 1m//s.
A rod OA is suspended with the help of a massless string AB as shown in figure. Rod is hinged at pointO. Draw free body diagrame of the rod.
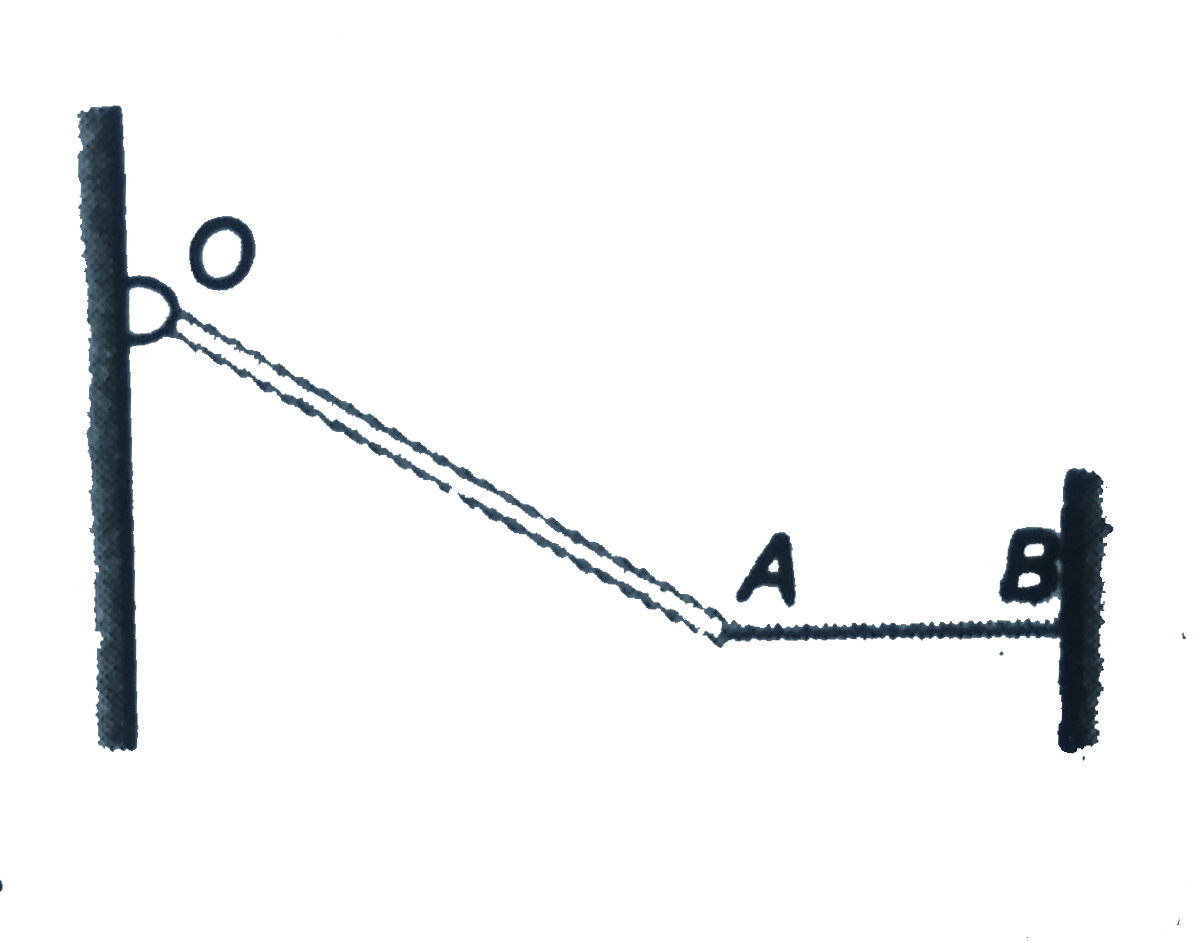
View SolutionA rod OA is suspended with the help of a massless string AB as shown in figure. Rod is hinged at pointO. Draw free body diagrame of the rod.

View SolutionA ring of mass M is kept on w horizontal rough surface . A force F is applied tangentially at its rim as shown . The coefficient of friction between the ring and surface is μ Then

View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View Solution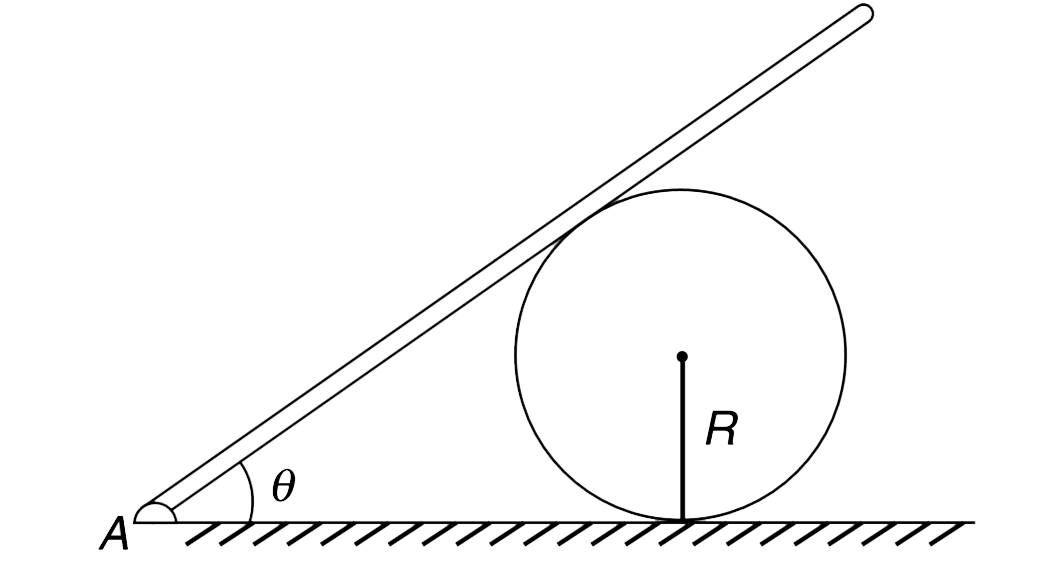
A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length L=2√3R is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if θ=60∘. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring.
View Solution
