
A river of width d is flowing with a velocity u. A person starts from point A. He always try to keep himself along y axis. Speed of man w.r.t to river at any position is given by v=k√y(k→+ve constant). Time taken by man to cross the river is (Assume that at t=0,y=0)
√dk
2√dk
2√dk
2d√k
The correct Answer is:C
t=∫dyVy=d∫0dyKy1/2=2√dk
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
A river of width 100 m is flowing with a velocity of 1.5 m/s. A man start from one end with rest relative the river. He raws with an acceleration of 2m/s2 relative to the river. If the man want to cross the river in minimum time, by how much distance (in meters) will he be drifted (flown) in the direction of river flow during the crossing.
View SolutionA river of width ω is flowing with a uniform velocity v. A boat starts moving from point P also With velocity v relative to the river. The direction of resultant velocity is always perpendicular to the line joining boat and the fixed point R. Point Q is on the opposite side of the river. P, Q and R are in a straight line. If PQ=QR=ω, find (a) the trajectory of the boat, (b) the drifting of the boat and (c) the time taken by the boat to cross the river.
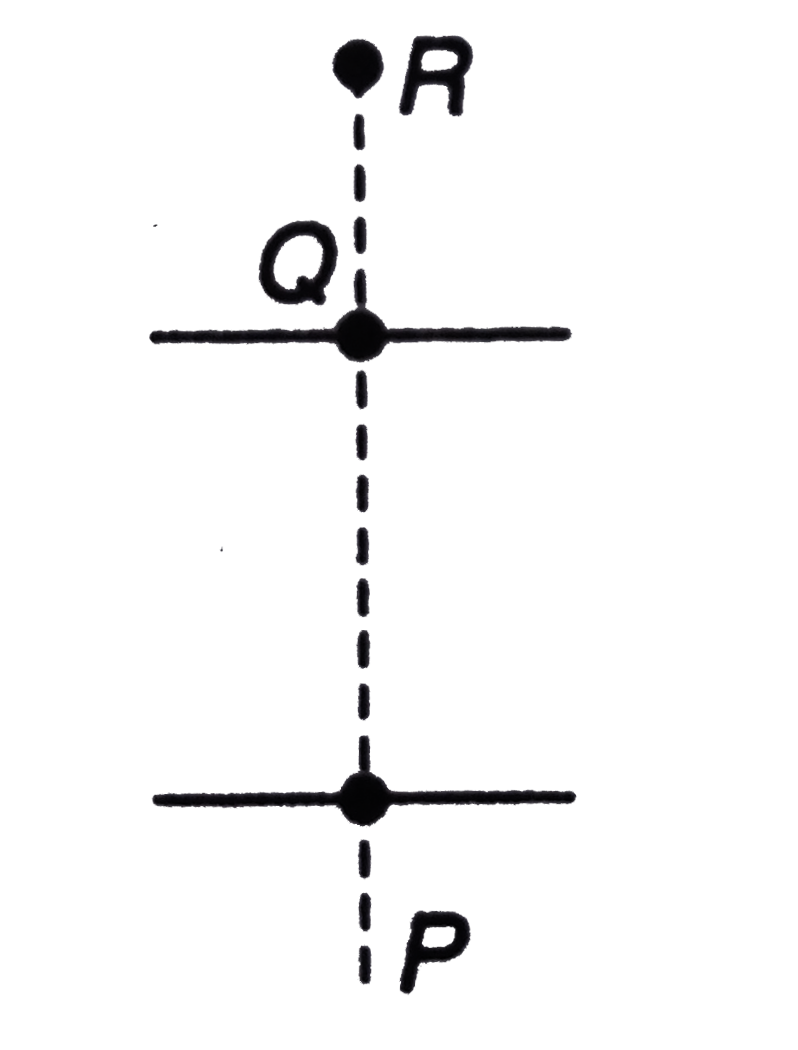 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A man at point A directs his rowboat due north toward point B, straight across a river of width 100 m. The river current is due east. The man starts across, rowing steadily at 0.75 m/s and reaches the other side of the river at point C, 150 m downstream from his starting point.
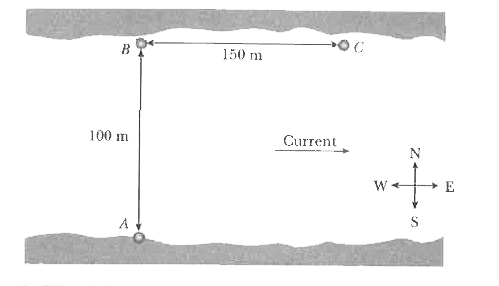
While the man is crossing the river, what is his velocity relative to the shore?A1.35 m/s, 34∘ north of eastB2.11 m/s, 34∘ north of eastC2.00 m/s, 56∘ north of eastD1.74 m/s, 34∘ north of east - Question 2 - Select One
A man can swim at a speed of 5 km/h W.r.t water. He wants to cross a 1.5 km wide river flowing at 3 km/h. He keeps himself always at an angle of 60° with the flow of direction while swimming, The time taken by him to cross the river will be
A0.26 hrB0.35 hrC0.45 hrD0.55 hr - Question 3 - Select One
A swimmer crosses a river of width d flowing at velocity v. While swimming, he keeps himself always at an angle of 120∘ with the river flow and on reaching the other end. He finds a drift of d/2 in the direction of flow of river. The speed of the swimmer with respect to the river is :
A(2−√3)vB2(2−√3)vC4(2−√3)vD(2+√3)v
A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.View SolutionA man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?View SolutionA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
View Solution
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. Suppose the boat wants to cross the river from A to the other side in the shortest possible time. Then what should be the direction of the velocity of boat relative to river?View SolutionA man can swim at a speed of 3kmh−1 in still water. He wants to cross a 500−m wide river flowing at 2kmh−1. He keeps himself always at an angle to 120∘ with the river flow while swimming.
The time taken to cross the river is.View Solution

