Let I1:(logx2)(log2x2)(log24x)>1
I2:x(log10x)2−3(log10x)+1>1000
and solution of inequality I1 is (1a√a,1b)∪(c,a√a)
and solution of inequality I2 is (d,∞) then answer the following
Sum of 'd' term of a GP whose common ratio is 1a and first term is c is more than
A
1
B
2
C
32
D
0
Video Solution
Text Solution
The correct Answer is:A, C, D
log2x=t
1t.11+t.(2+t)>1
2+tt2+t>1
1−2+tt2+t<0
t2−2t(t+1)<0
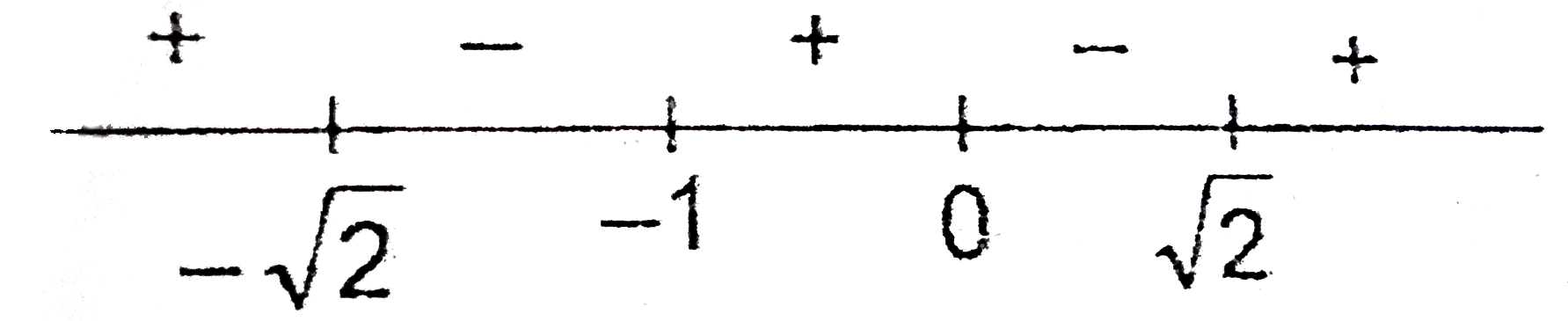
−√2<t<−1 or 0<t<√2
2−√2<x<12 or 1<x<2√2
x∈(12√2,12)∪(1,2√2)
I2:log10x=t
(t3−3t+1)t>3
t3−3t2+t−3>0
(t−3)(t2−1)>0
t>3
x>1000
a=2,b=2,c=1,d=1000
Sol.2. Sum of GP=1−(12)10001−12
=2(1−121000)
|
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Math
105 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - MATHEMATICS
263 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - I MATHEMATICS SEC - 2
1 Videos
- TEST PAPERBOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY
37 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS
131 Videos
Similar Questions
Knowledge Check
Let I1:(logx2)(log2x2)(log24x)>1
I2:x(log10x)2−3(log10x)+1>1000
and solution of inequality I1 is (1a√a,1b)∪(c,a√a)
and solution of inequality I2 is (d,∞) then answer the following
Both root of equation dx2−bx+k=0,(k∈R) are positive then k can not beA12B13C1D2Solution set of x(log10x)2−3log10x+1>1000 for xεR is
A(10,∞)B(100,∞)C(1000,∞)D(1,∞)Let solution of inequality 161x2x+3>1 is (−∞,a)∪(b,c) then
Aa2+b2+9c2=25Ba+b+c>0Ca2+b2+c2=17Da+b+c<0
Solve the following inequation .
(xv) x(log10x)2−3log10x+1>1000
View SolutionThe solution of the inequality logx(4x2−1)<2, is
View Solutionlog10x−12log10(x−12)=log10(x+12)−12log10(x+18)
View SolutionThe solution of the inequality log12sin−1x>log12cos−1x is
View SolutionThe solution set of the inequality logx(x+31−2x)>1 is
View Solution
