One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
The correct Answer is:TB=600×23/5K,
TD=1200×2−3/5K,η=61.37%
The corresponding P−V diagram is as shown
Given : TA=300K,n=1,γ=1.4,VA/VB=16
andVC/VB=2LetVB=V0andPB=P0ThenVC=2V0andVA=16V0TemperatureatBB
Process A−B is adiabatic. Hence
TAVγ−1A=TBVγ−1B
or TB=TA(VAVB)γ−1
=(300)(16)1.4−1
=600×23/5K,
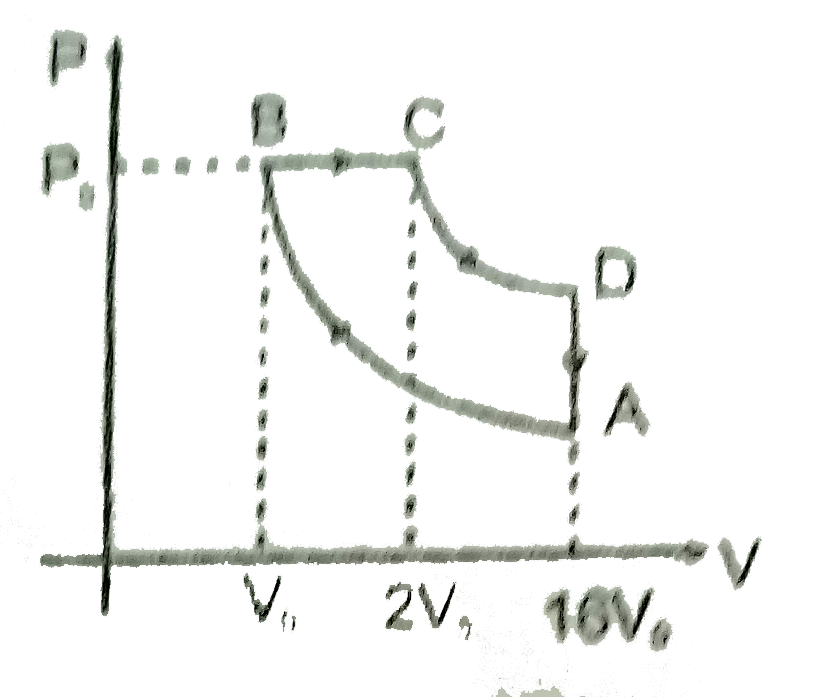
Temperature at D
B→C is an isobaric process (P= constant)
∴T∝V
VC=2VB
∴TC=2TB=(2)600×23/5K
TC=1200×23/5K
Now the process C−D is adiabatic.
Therefore
∴TD=TC(VCVD)γ−1=1200×23/5(216)1.4−1
TD=1200×23/5K,
Efficiency of cycle-
Efficiency of cycle (in percentage) is defined as
η=Net work doen in the cycleHeta absorbed in the cycle×100
η=WTotalQ+ve×100
=Q+ve=−Q−veQ+ve×100=(1−Q1Q2)×100...(1)
where Q1= Negative heat in the cycle (heat released)
and Q2= Positive heat in the cycle (heat absorbed) In the cycle-
QAB=QCD=0 (Adiabatic process)
In process DA:ΔQ=ΔU+ΔW(ΔW=0)
QDA=nCvΔT=(1)(52R)(TA−TD)(Cv=52R for a diatomic gas)
=52×8.31(300−791.7)J
[TD=1200×23/5K=791.K]
or QDA=−10215.06J (Release)
and QBC=nCPΔT=(1)(72R)(TC−TB)(CP=72R for a diatomic gas)
=(72)(8.31)(181.8−909.4)J
[TD=1200×23/5K≈1818.8K,TB=600×23/5≈909.4K]
or QBC=26449.89J
Therefore, substituting Q1=10215.06J and Q2=26449.89J in diatomic (1) we get-
∴η={1−10215.0626449.89}×100
or η=61.37%
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - Advancel Level Problems
1 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCECHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCECHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
65 Videos
Similar Questions
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionA monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown figure. The volume rations are VBVA=2andVDVA=4 If the temperature fTAatAis27∘C.
 Calculate,
Calculate,
View Solution
Knowledge Check
An ideal mono atomic gas is taken through the cyclic process shown in fig. Linear expansion from A to B following by adiabatic compression back to original state
 AEfficiency of cyclic process is zeroBDuring process A to B heat is released onlyCDuring process A to B heat is absorbed onlyDDuring linear process heat enters and leaves the process
AEfficiency of cyclic process is zeroBDuring process A to B heat is released onlyCDuring process A to B heat is absorbed onlyDDuring linear process heat enters and leaves the processOne mole of an ideal gas is taken through a cyclic process as shown in the V-T diagram. Which of the following statements is true ?
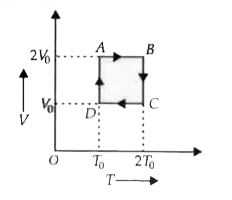 AThe magnitude of work done by the gas is RT0ln2.BWork done by gas is V0T0CNet work done by the gas is zero.DWork done by the gas is 2RT0ln2.
AThe magnitude of work done by the gas is RT0ln2.BWork done by gas is V0T0CNet work done by the gas is zero.DWork done by the gas is 2RT0ln2.A monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate.
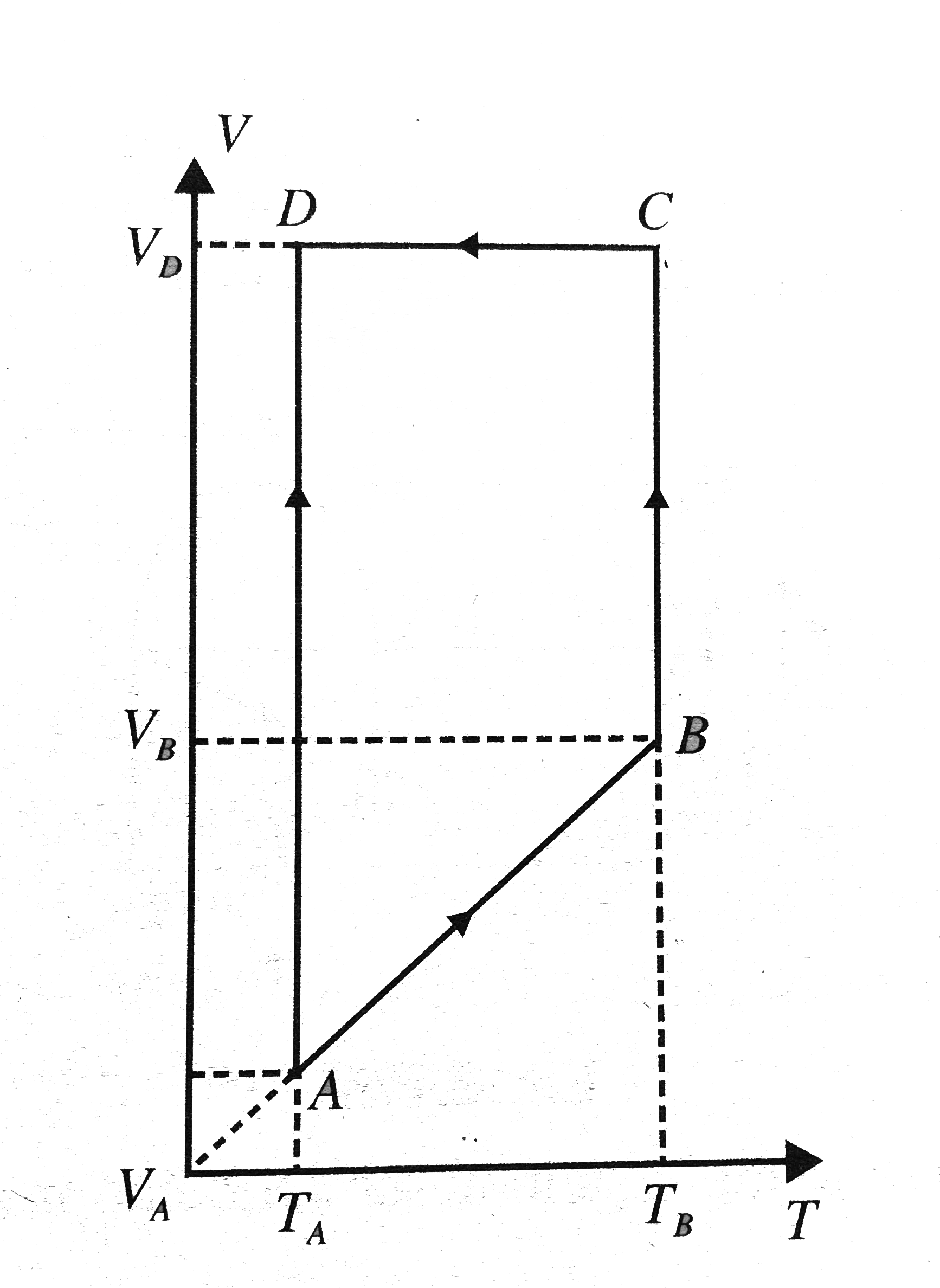
The temperature of the gas at point BA500KB700KC600KD300K
A mono-atomic ideal gas of two moles is taken through a cyclic process starting from A as shwon in the figure below.
The volume ratios are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C. Calculate
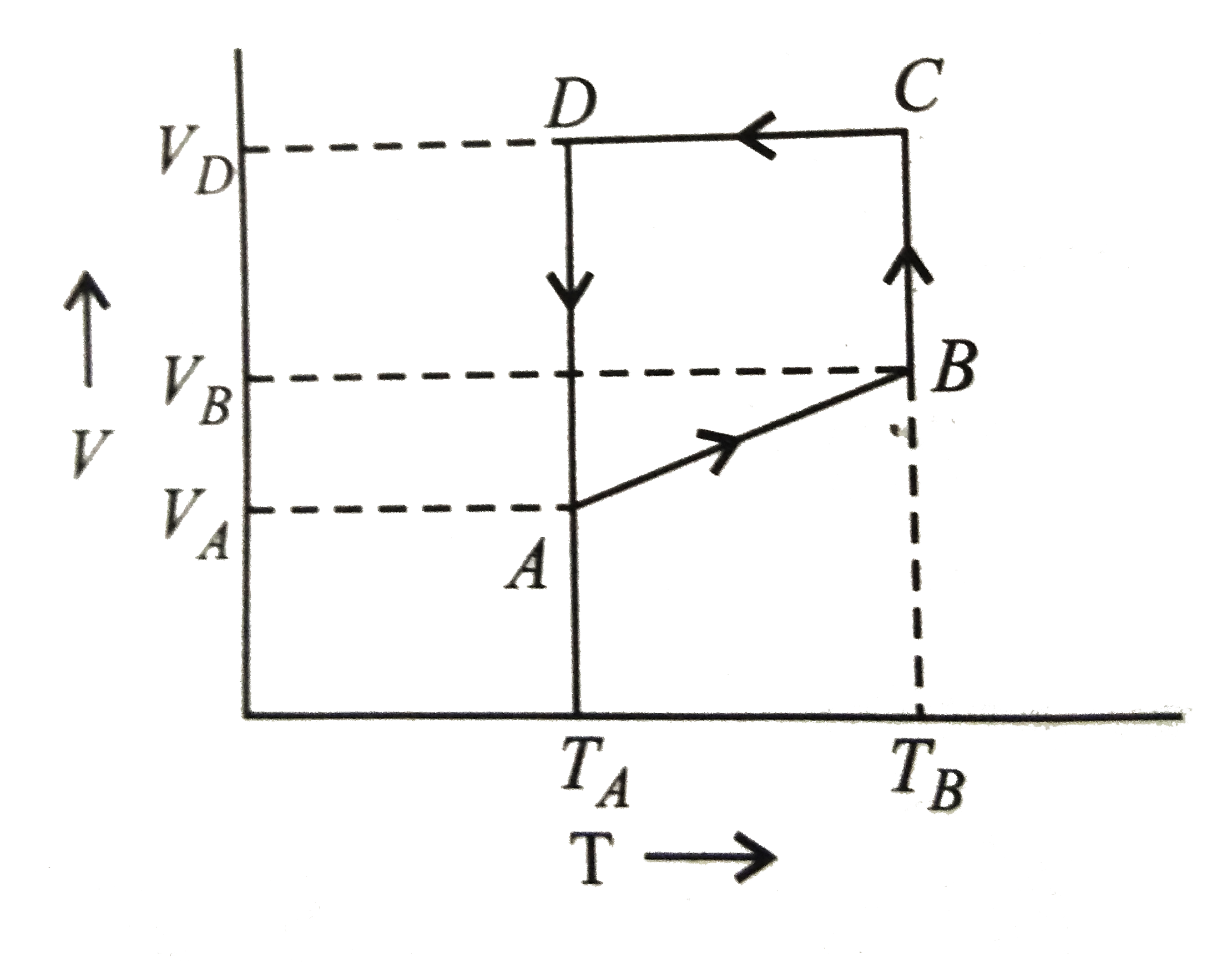
a. The temperature of gas at B.
b. Heat absorbed or evolved in each process.
c. Total wrok done in cyclic process.
View SolutionA monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown in figure. The volume ratios are VBVA=2andVDVA=4. If the temperature TA at A is 27∘C.
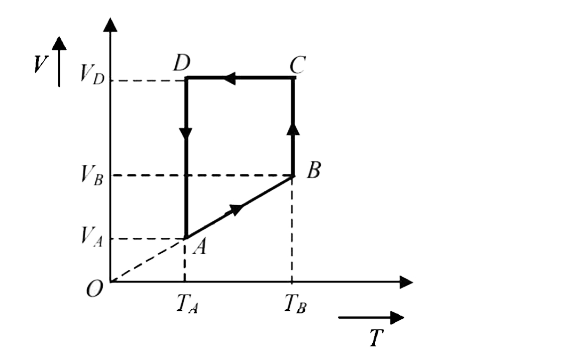
Calculate,
(a) the temperature of the gas at point B,
(b) heat absorbed or released by the gas in each process,
(c) the total work done by the gas during the complete cycle. Express your answer in terms of the gas constant R.
View SolutionA monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown in figure. The volume ratios are VBVA=2 and VDVA=4. If the temperature TA at A is 27∘C, calculate:
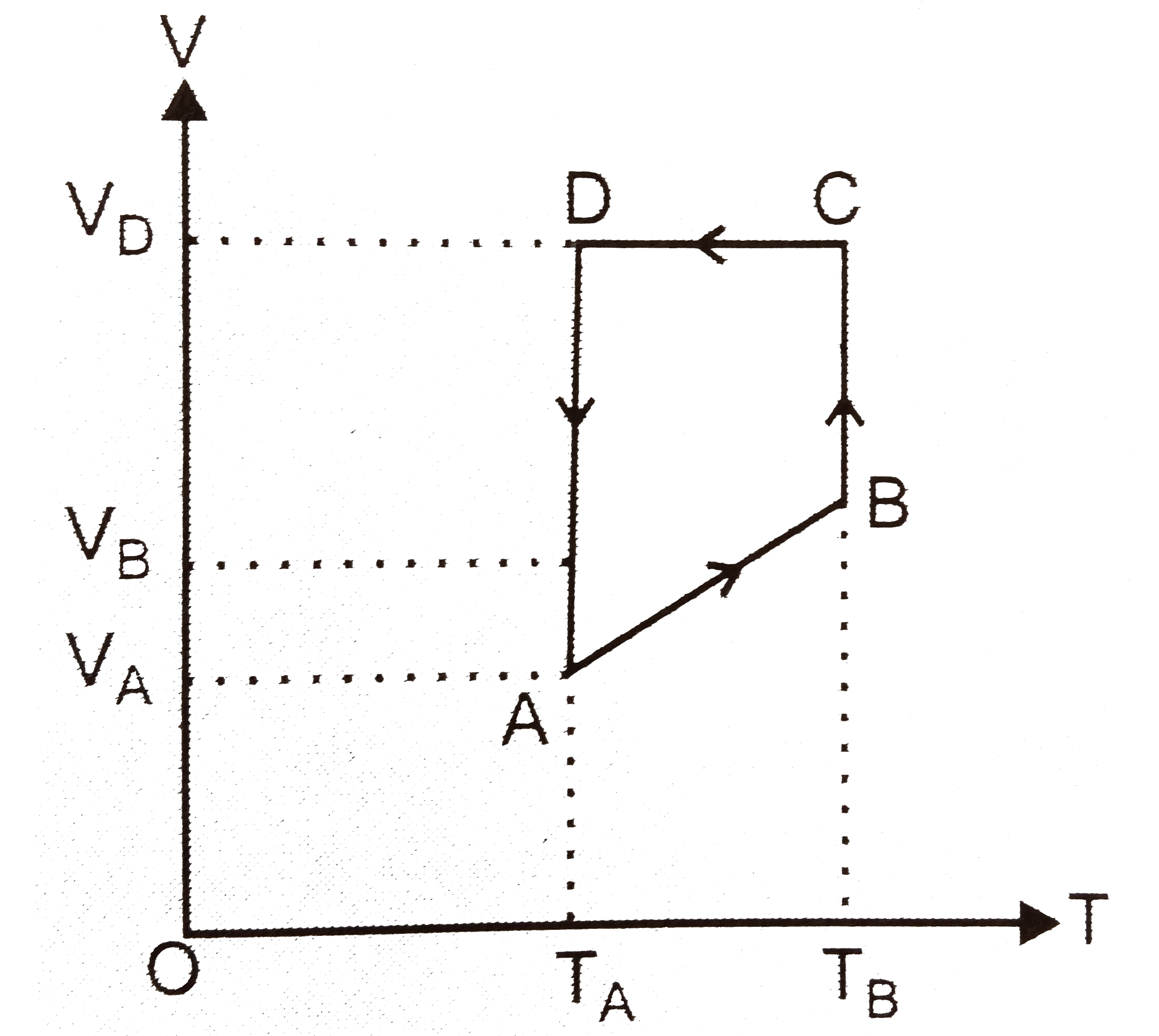
(a) The temperature of the gas at point B.
(b) Heat absorbed or released by the gas in each process.
(c) The total work done by the gas during complete cycle.
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
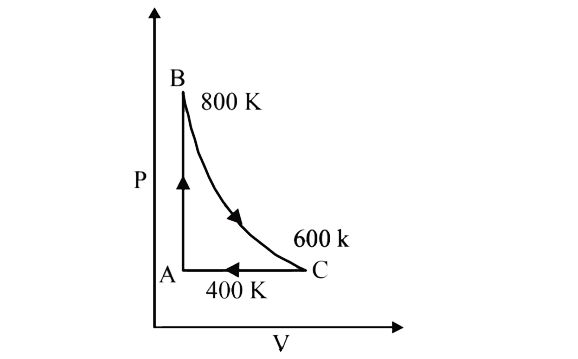
View SolutionA monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate.
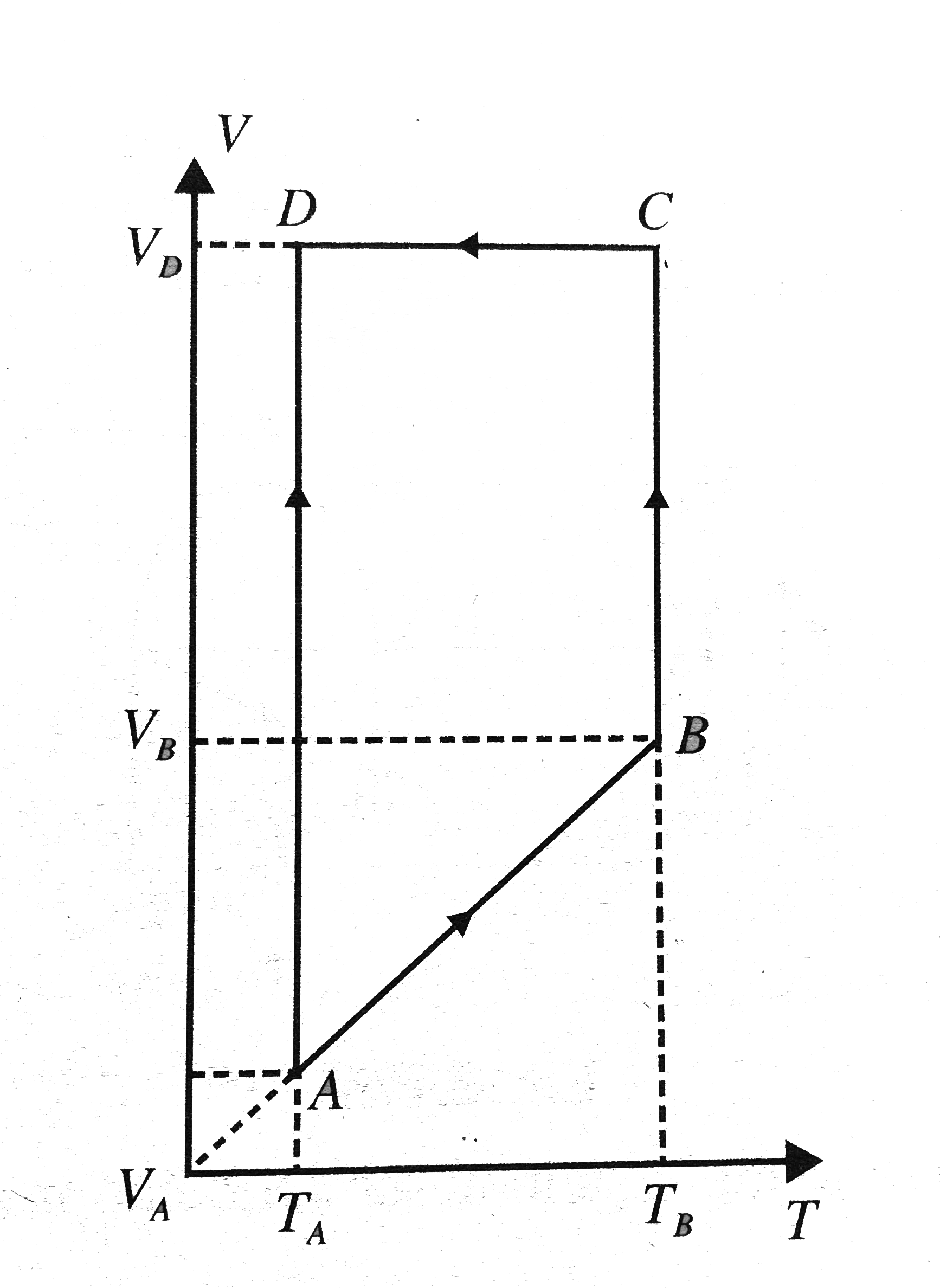
The total work done by the gas during the complete cycle.
View Solution
