A Carnot engine cycle is shown in the Fig. (2). The cycle runs between temperatures $T_{H} = α T_{L} = T_{0} (α > T)$ . Minimum and maximum volume at state $1$ and states $3$ are $V_{0}$ and $n V_{0}$ respectively. The cycle uses one mole of an ideal gas with $C_{P} / C_{V} = γ$ . Here $C_{P}$ and $C_{V}$ are the specific heats at constant pressure and volume respectively. You must express all answers in terms of the given parameters ${α, n, T_{0}, V_{0} ?}$ and universal gas constant $R$ .
(a) Find $P, V, T$ for all the states
(b) Calculate the work done by the engine in each process: $W_{12}, W_{23}, W_{34}, W_{41}$ .
(c) Calculate $Q$ , the heat absorbed in the cycle.

Video Solution

Text Solution

Verified by Experts

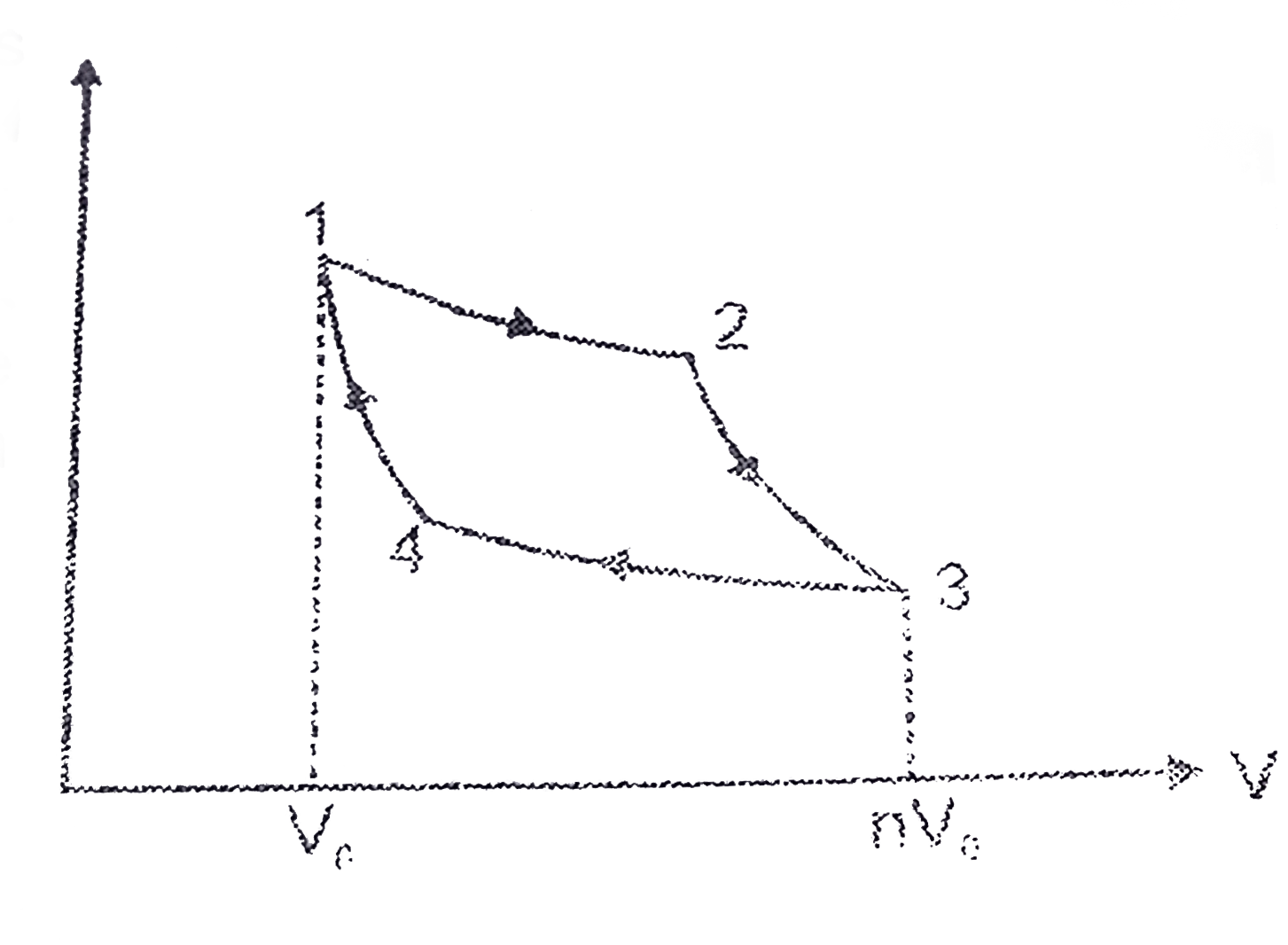
$P_{1} = \frac{R α T_{0}}{V_{0}}, P_{2} = \frac{α^{\frac{γ}{γ - 1}} R T_{0}}{n V_{0}}$
$P_{3} = \frac{R T_{0}}{n V_{0}}, P_{4} = \frac{R T_{0}}{α^{\frac{1}{γ - 1}} V_{0}}$
$V_{1} = V_{0}, V_{2} = \frac{n V_{0}}{α^{\frac{1}{γ - 1}}}$
$V_{3} = n V_{0}, V_{4} = α^{\frac{1}{γ - 1}} V_{0}$
$T_{1} = α T_{0}, T_{2} = α T_{0}$
$T_{3} = T_{0}, T_{4} = T_{0}$
(b) $W_{12} = - \frac{R}{γ - 1} (T_{0} - α T_{0})$
$W_{34} = R T_{0} ⎛ ⎜ ⎝ \frac{α^{\frac{1}{γ - 1}}}{n} ⎞ ⎟ ⎠$
$W_{41} = - \frac{R}{γ - 1} (α T_{0} - T_{0})$
(c ) $Q = R T_{0} (α - 1) ln ⎛ ⎝ \frac{n}{α^{(\frac{1}{γ - 1})}} ⎞ ⎠$

Updated on:21/07/2023

$C_{v} and C_{p}$ denote the molar specific heat capacities of a gas at constant volume and constant pressure, respectively. Then
A $C_{p} + C_{v}$ is larger for a diatomic ideal gas than for a monoatomic ideal gas.
B $C_{p} - C_{v}$ is larger for a diatomic ideal gas ghtan for a monoatomic ideal gas.
C $C_{p} . C_{v}$ is larger for a diatomic ideal gas than for monoatomic ideal gas.
D $C_{p} / C_{v 0}$ is larger for a diatomic ideal gas than for a monoatomic ideal gas.
When water is heated from $0^{\circ} C$ to $4^{\circ} C$ and $C_{P}$ and $C_{V}$ are its specific heats at constant pressure and constant volume respectively , then :-
A $C_{P} > C_{V}$
B $C_{P} < C_{V}$
C $C_{P} = C_{V}$
D $C_{P} - C_{V} = R$
For one mole of an ideal gas $(C_{p} and C_{v}$ are molar heat capacities at constant presure and constant volume respectively)
A $C_{p} - C_{v} = R$
B $C_{p} - C_{v} = \frac{R}{2}$
C $C_{p} - C_{v} = - 2 R$
D $C_{p} - C_{v} = 0$