A mass of 8g of oxygen at the pressure of one atmosphere and at temperature 27∘C is enclosed in a cylinder fitted with a frictionless piston. The following operations are performed in the order given (Specific heat fo oxygen cV=670J/kgK, Molecular mass of oxygen =32gm/mole, one atm =1.013×105N/m2 and R=25/3J/mole−K)
(a) the gas is heated at constant pressure to 127∘C,
(b) then it is compressed isothermally to its initial volume and
(c ) finally it is cooled to its initial temperature at constant volume.
Find the heat absorbed by the gas during operation (a) ?
Find work done by the gas in case (a)?
Find the work done on the gas in case (b)?
Find the heat extracted from the gas in case (c )?
The correct Answer is:A, B, C, D
for enclosed gas number of moles
n=832=14 mole
From gas equation for process (a)
P0ViTi=P0VfTf⇒ViVf=300400=34
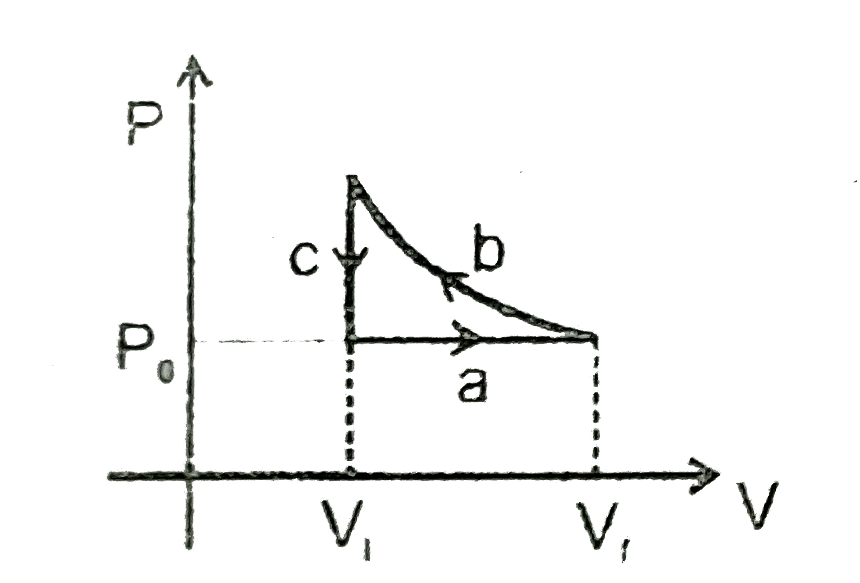
(1) Heat absrobed by the gas during operation 'a'
Q=nCPΔT=14[6701000×32+253]×100=893∘12J
(2) Work done by the gas in case 'a'
W=nRΔT=14×253×100=6253J
(3) Work done by the gas in case 'b'
W=nRTloge(VfVi)=14253×400ln(4/3)
=25003ln(4/3)
(4) Heat extracted form the gas in case 'c'
Q=nCvΔT=14×6701000×32×100=536J
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - Advancel Level Problems
1 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCECHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCECHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
65 Videos
Similar Questions
One mole of oxygen is heated at constant pressure starting at 0∘C. How much heat energy must be added to the gas to double its volume ?
View SolutionA container is filled with one gram mole oxygen at a pressure of one atom and temperature 27∘C. It is assumed that molecules of the gas are moving with velocity vrms' then vrms will be-
( Atoms =105N/m2andK=1.38×10−23J/K)
View Solution
Knowledge Check
If one mole of an ideal gas with Cv=32R is heated at a constant pressure of 1 atm 25∘C to 100∘C. Which is correct
AΔU during the process is 223.51 calBΔH during the process is 372.56 calCentropy change during the process is 1.122calk−1mol−1DΔU,ΔH are same for the process0.5 mole of diatomic gas at 27∘C is heated at constant pressure so that its tripled. If =8.3Jmole−1k−1 then work done is
A4980JB2490JC630JD1345JLiquid oxygen at 50K is heated to 300K at constant pressure of 1atm. The rate of heating is constant. Which of the following graphs represents the variation of temperature with time?
A B
B C
C D
D
Five moles of oxygen gas is heated from 40°C to 70°C at constant pressure Heat given to the gas will be (given R 2 cal/mol K)
View SolutionHalf mole of an ideal monoatomic gas is heated at constant pressure of 1 atm from 20∘C to 90∘C. Work done by gas is close to: (Gas constant R = 8.31 J/mol-K)
View SolutionCompressed oxygen is sold at a pressure of 100 atmosphere in a cylinder of 49 litre. The number of moles of oxygen in the cylinder is:
View SolutionThe kinetic energy of translation of 20gm of oxygen at 47∘C is (molecular wt. of oxygen is 32 gm/mol and R=8.3 J/mol/K)
View SolutionA gas placed in a cylinder fitted with a frictionless piston expands against a constant external pressure of 1 atm from a volume of 10 litre to 15 litre by absorbing 400 J heat. The change in internal energy is
View Solution
