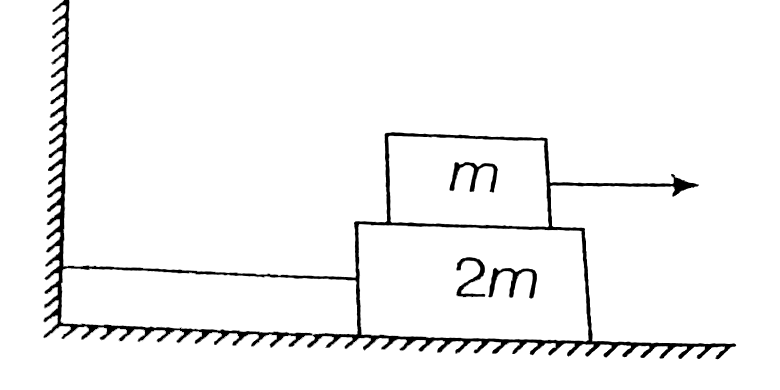
A two block system is shown in figure . We shall draw complete free body diagram and find normal reaction between m1andm2 and between m2 and ground .
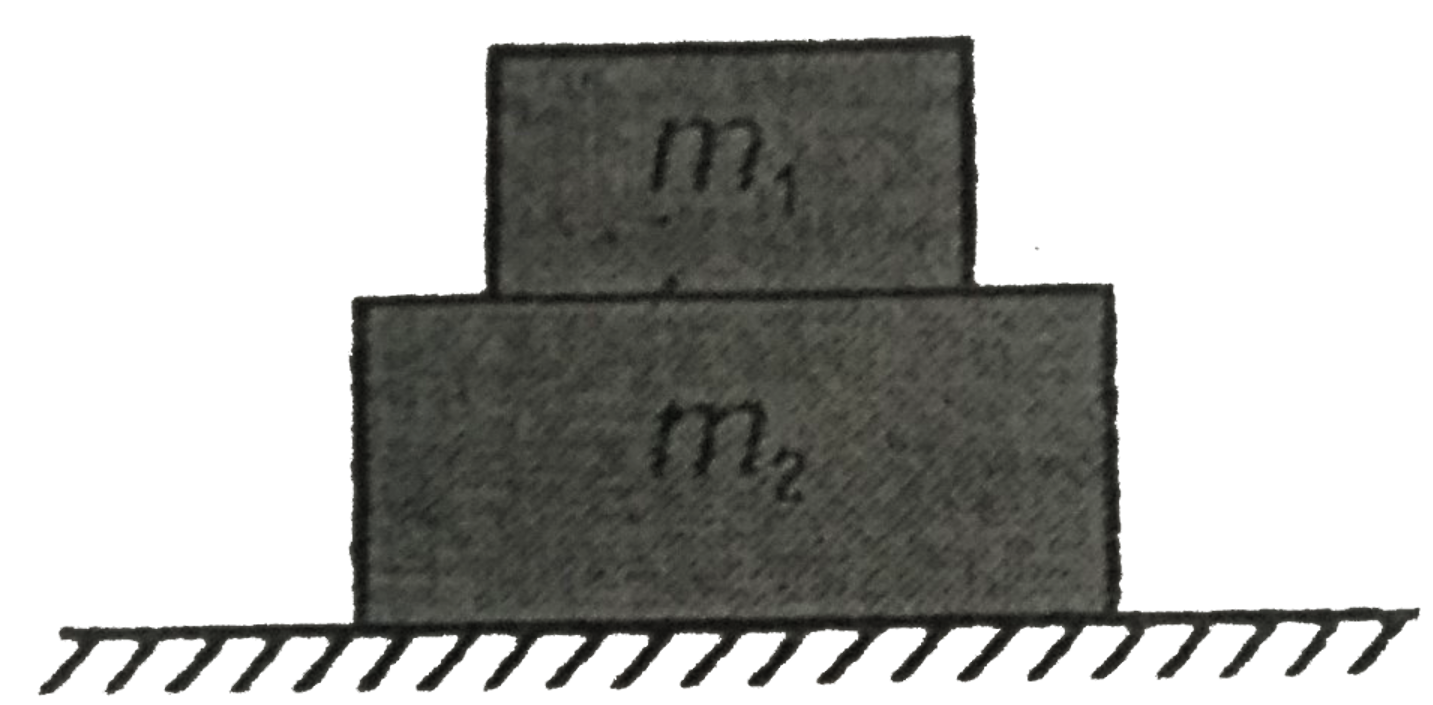
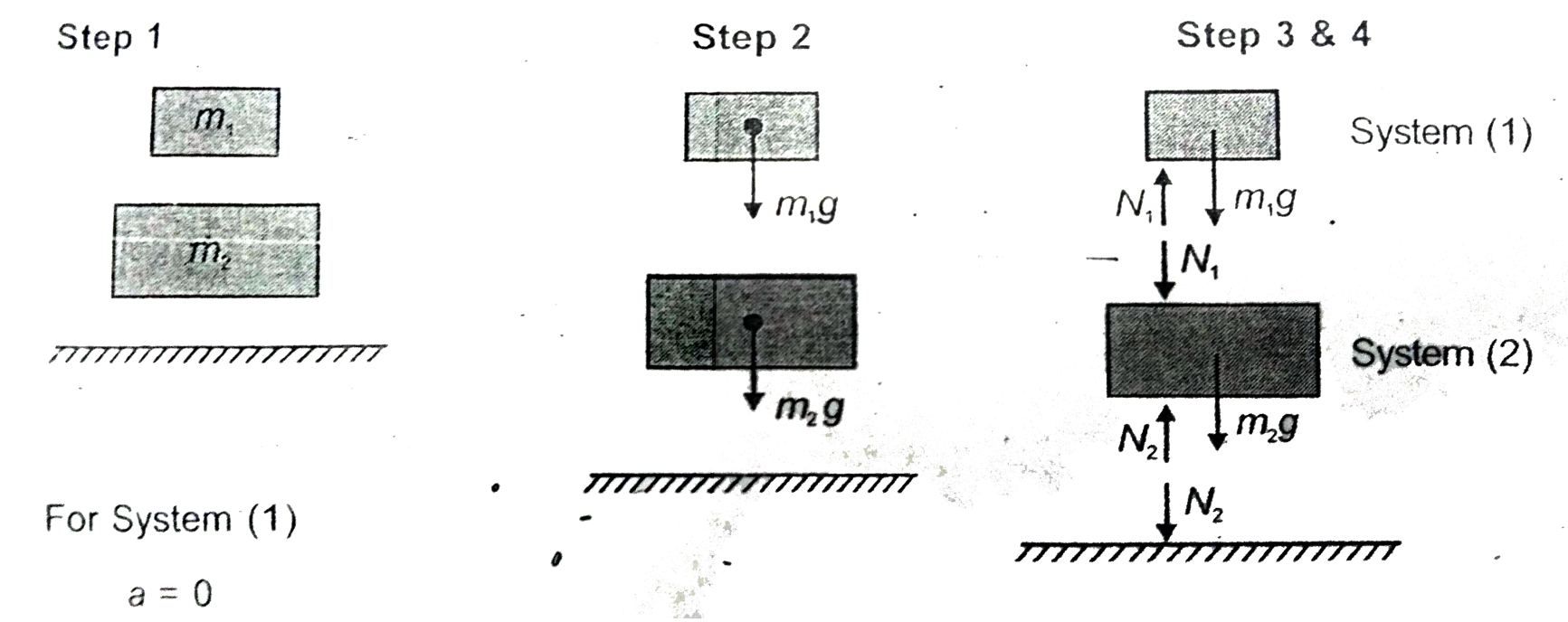 For system (1)
For system (1)
a=0
From Newto's 2nd law,
N1−m1g=m1(0)
N1=m1g …(i)
N2−(N1+m2g)=m2(0)
⇒N2=N1+m2g
⇒N2=(m1+m2)g [∵From(i),N1=m1g)]
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - TRY YOURSELF
67 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -A)
48 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTECHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
In the figure masses m1,m2andM are 20 kg, 5 kg and 50 kg, respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1andM and that between m2 and ground is 0.3. The pulleys and the string are massless.
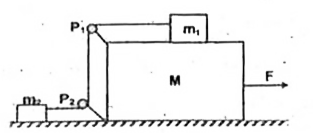
The string is perfectly horizontal between P1 and m1 and also between P2andm2. The string is perfectly vertical between P1andP2. An external horizontal force F is applied to the mass M. Take g=10m/s2.
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1andM be f1 and that between m2 and ground be f2. For a particular F, it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
View SolutionA blocked of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

View Solution
Knowledge Check
If system is in equilibrium then find relation between m1 and m2
 Am1m2=12Bm1m2=115Cm1m2=110Dm1m2=1
Am1m2=12Bm1m2=115Cm1m2=110Dm1m2=1Two blocks of mass m1=6kg and m2=3kg are as shown in the diagram. Coefficient of friction between m1 and m2 and between m1 and m2 and between m1 and the surface is 0.5 and 0.4 , respectively . The maximum horizontal force that can be applied to the mass m1 so that they move without separation is
 A41NB61NC81ND101N
A41NB61NC81ND101NTwo blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m1 and platform is 2μ and that between block m2 and platform is μ.The platform moves with an acceleration a . The normal reation between the blocks is
 Azero in all casesBzero only if m1=m2Cnon zero only if a>2μgDnon zero only if a>μg
Azero in all casesBzero only if m1=m2Cnon zero only if a>2μgDnon zero only if a>μg
Two blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



View SolutionIn the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

View SolutionIn the figure masses m1,m2 and M are kg. 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
View SolutionIn the figure , masses m1,m2 and M are 20 kg , 5 kg and 50 kg respectively . The coefficient of friction between M and ground is zero . The coefficient of friction between m1 and M and that between m2 and ground is0.4 . The pulleys and the string are massless . The string is perfectly horizontal between P1 and m1 and also between P2 and m2 . The string is perfectly vertical between P1 and P2 . An external horizonal force F is applied to the mass M . (Take g = 10m/s2)
(a) Draw a free body diagram for mass M , clearly showing all the forces .
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2 . For a particular F it is found that f1=2f2 . Find f1 and f2 . Write down equation of motion of all the masses . Find F , tension in the string and acceleration of the masses .

View SolutionTwo blocks of masses m and 2 m are placed one over the other as shown in figure.The coefficient of friction between m and 2m is μ and between 2m and ground is μ3. If a horizontal force F is applied on upper block and T is tension developed in string, then choose the incorrect alternative.
View Solution
