A particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
3sinα=2cosβ
2sinα=3cosβ
3sinβ=2cosα
2sinβ=3cosα
The correct Answer is:C
(C) Let v be the speed of particle at B, just when it is about to loose contact.
From application of Newton's second law to the particle normal to the spherical surface.
mv2r=mgsinβ....(1)
Applying conservation of energy as the block moves from A to B.
12mv2=mg(rcosα−rsinβ)....(2)
Solving 1 and 2 we get
3sinβ=2cosα
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 445videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 457videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 427videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA particle of mass m is placed in equlibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical wheere cosθ35. if the work done against frictiion is 2mgR10x, find x.
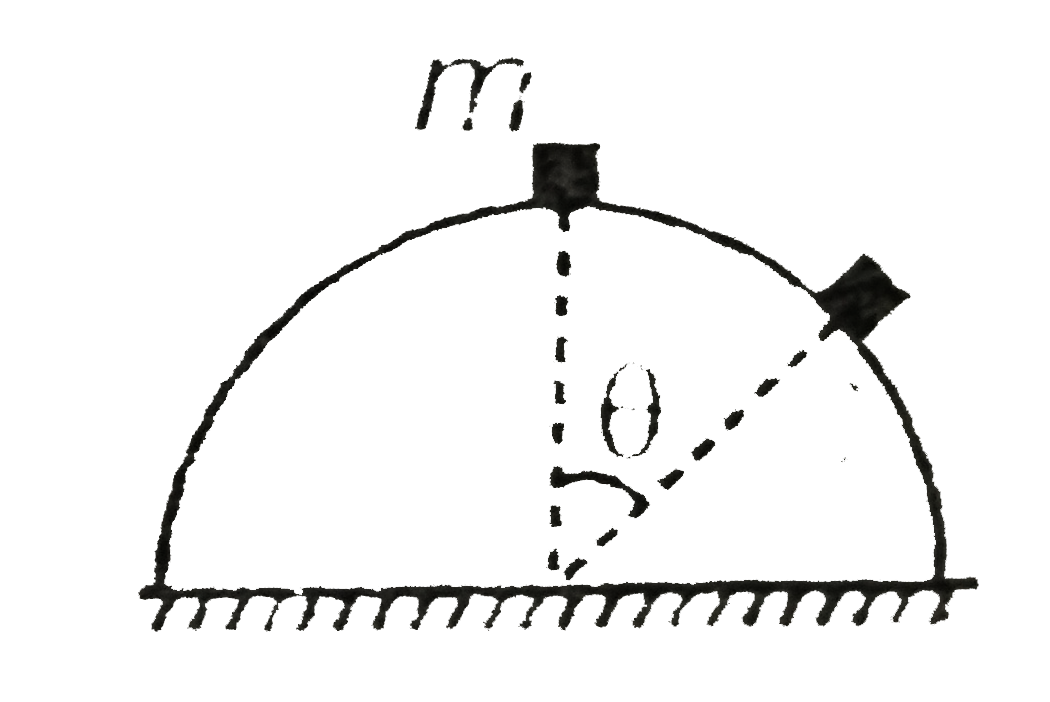 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle of mass m is going along surface of smooth hemisphere of radius R in verticle plane. At the moment shown its speed is v. Choose correct option(s).
 Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)
Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ) - Question 2 - Select One
A practical moves from rest at A on the surface of a smooth circular cylinder of radius r as shown . At B it leaves the cylinder. The equation relating αandβ is
 A3sinα=2sinβB2sinα=3cosβC3sinβ=2cosαD2sinβ=3cosα
A3sinα=2sinβB2sinα=3cosβC3sinβ=2cosαD2sinβ=3cosα - Question 3 - Select One
A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
A particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View SolutionA block of mass as shown is released from rest from top of a fixed smooth hemisphere. Find angle made by this particle with vertical at the instant when it looses contact with hemisphere.
 View Solution
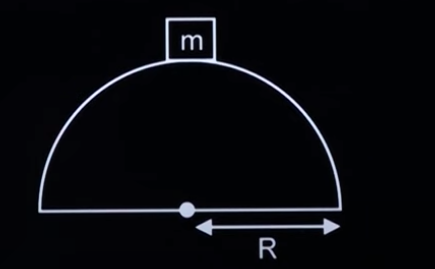
View SolutionA small block of mass m starts sliding down from rest along the smooth surface of a fixed hollow hemisphere of same mass m. Find the distance of centre of mass of block and hemishere from centre of hemisphere C when block m separates from the surface of hemisphere.
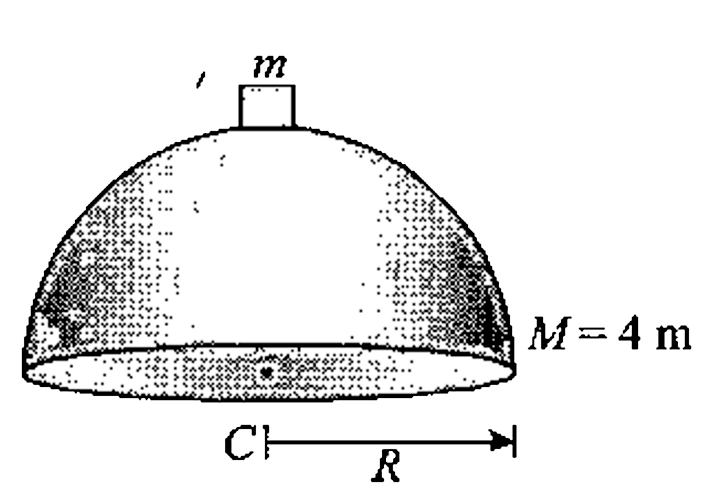 View Solution
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 View Solution
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
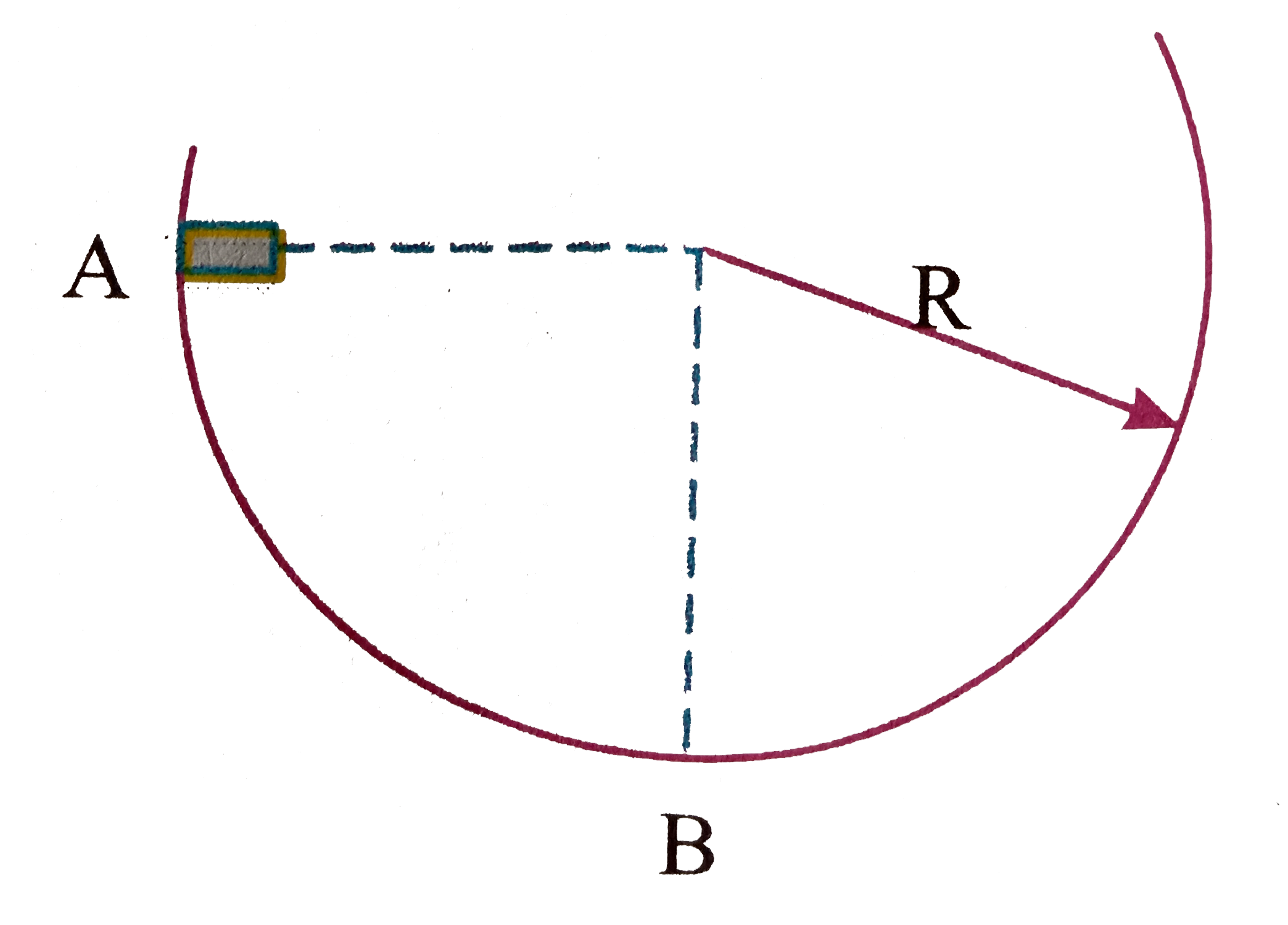 View Solution
View Solution

