A bob is attached to one end of a string other end of which is fixed at ped A. The bob is taken to a position where string makes an angle of 30∘ with the horizontal. On the circular path of the bob in vertical plane there is a peg'B' at a symmetrical position with respect to the position of release as shown in the figure. If Vc and Va be the minimum speeds in clockwise and anticlokwise direction respectively, given to the bob in order to hit the peg 'B' then ratio Vc:Va is equal to :

1:1
1:√2
1:2
1:4
The correct Answer is:C
(C) For anti− clockwise motion, speed at the highest point should be √gR. Conserving energy at (1)&(2):
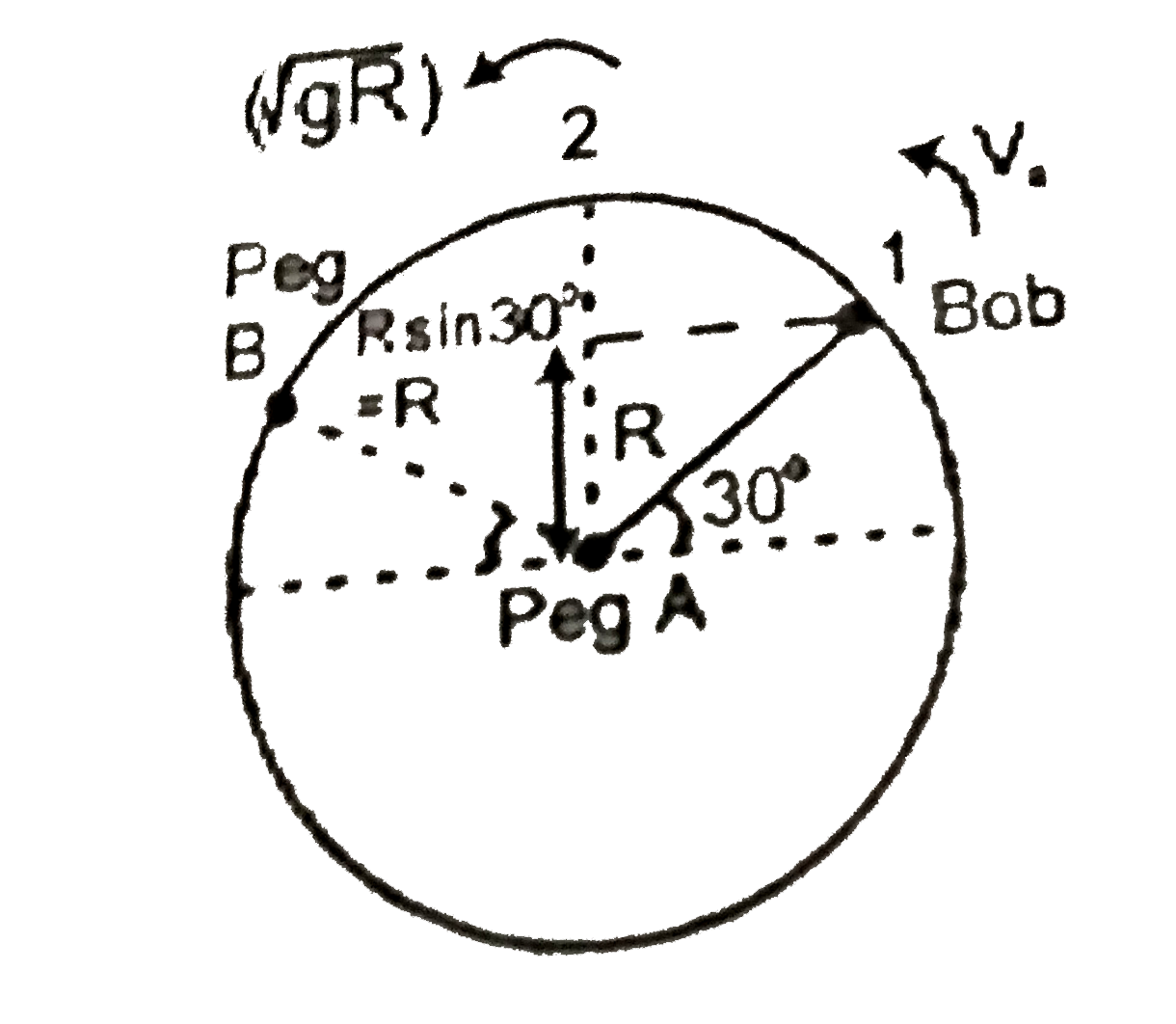
12ma2a=mgR2+12m(gR)
⇒v2a=gR+gR=2gR
⇒va=√2gR
For clock− wise motion, the bob must have atleast that much speed initially, so that the string must not become loose any where until it reaches the pegB. At the initial position :
T=mgcos60∘=mv2cR,VC being the intial speed in clockwise direction.
For Vcmin:Put T=0,
VCmin:T=0
⇒VC=s√gR2
⇒VC/Va=√gR2√2gR=12 Ans.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 505videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 517videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 484videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A bob of mass 2 kg hangs from a string of length 5 m . It swings from its rest position to one of the sides so that the string makes an angle of 60∘ with the vertical Calculate the gain in potential energy of the bob .
View SolutionOne end of ideal string tied up with fixed suppot & other end is tied with a bob. The string is released from horizontal position. When string makes an angle of θ with vertically downward direction then the acceleration vector of bob is horizontal then θ is
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass m hangs at one end of a string of lenth l, the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at bottommost point position is
A2 mgBmgC3 mgD√3mg - Question 2 - Select One
A body of mass m hangs at one end of a string of length l , the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at mean position is
A2mgBmgC3mgD√3mg - Question 3 - Select One
A body of mass m hangs at one end of a string of length l, the other and of which is fixed . It is given a horizontal velocity so that the string would just reach where it makes an angle of 30∘ with the vertical . The tension in the string at mean position is
Amg(5−2√3)Bmg(3−3√3)Cmg(3−√3)Dmg(4−√3)
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
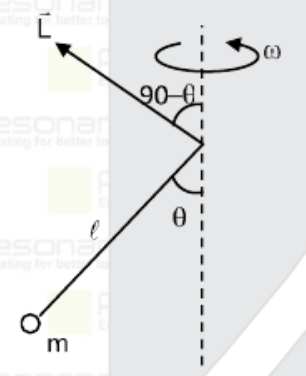 View Solution
View SolutionThe mass of a simple pendulum bob is 100 gm. The length of the pendulum is 1 m. The bob is drawn aside from the equilibrium position so that the string makes an angle of 60∘ with the vertical and let go. The kinetic energy of the bob while crossing its equilibrium position will be
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
View SolutionThe bob of a 0.2 m pendulum describes an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is
View SolutionThe bob hanging from a light string is projected horizontally with a speed u0. In the subsequent upward motion of the bob in vertically plane
 View Solution
View Solution

