A particle of positive charge q and mass m enters with velocity $V ˆ i$ at the origin in a magnetic field $B (- ˆ k)$ which is present in the whole space. The charge makes a perfectely inelastic collision with an identical particle (having same charge) ar rest but free to move at its maximum positive y-coordinate. After collision, the combined charge will move on trajectory where $r = \frac{m V}{q B}$ .

A

$y = \frac{m v}{q B} (- ˆ i)$

B

${(x + r)}^{2} + {(y - r / 2)}^{2} = r^{2} / 4$

C

${(x - r)}^{2} + {(y - r)}^{2} = r^{2}$

D

${(x - r)}^{2} + {(y + r / 2)}^{2} = r^{2} / 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

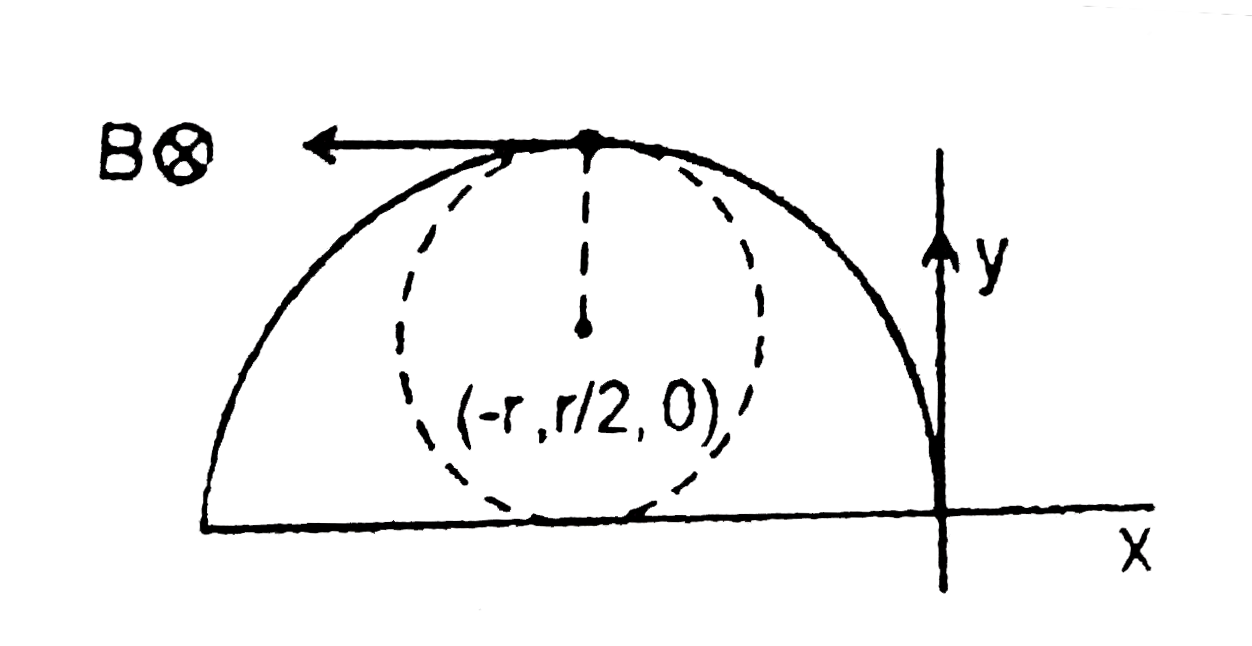Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A charged particle of charge $Q$ and mass $m$ moves with velocity $v$ in a circular path due to transverse magnetic field, B, then its frequency is
A $\frac{Q B}{2 π m}$
B $\frac{Q v B}{2 π m}$
C $\frac{Q m v B}{2 π}$
D $\frac{v b}{2 π Q m}$
Question 2 - Select One
A charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

AVelocity of the particle when it comes out form the magnetic field is $\to v - v {cos 60}^{\circ} ˆ i + v {sin 60}^{\circ} ˆ j$
BTime for which the particle was in magnetic field is $\frac{π m}{3 q B}$
CDistance travelled in magnetic field is $\frac{π m v}{3 q B}$
DNone of these
Question 3 - Select One
A charged particle of specific charge $α$ moves with a velocity $\to v = v_{0} ˆ i$ in a magnetic field $\to B = \frac{B_{0}}{\sqrt{2}} (ˆ j + ˆ k)$ . Then (specific charge=charge per unit mass)
Apath of the particle is a helix
Bpath of the particle is circle
Cdistance moved by the particle in time $t = \frac{π}{B_{0} α} i s \frac{π v_{0}}{B_{0} α}$
Dvelocity of the particle after time $t = \frac{π}{B_{0} α} i s (\frac{v_{0}}{2} ˆ j + \frac{v_{0}}{2} ˆ j)$

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.51

Home
Ask Doubt
Profile