A square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion. 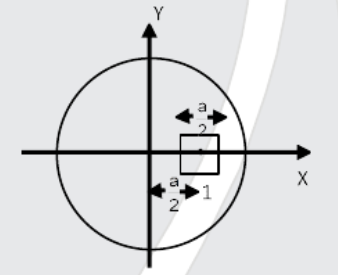
x=(−2aπe)
(−a8πe−2)
(−4a3πe)
(−a3πe−4)
The correct Answer is:B
Step by step video, text & image solution for A square of side a/2 is removed from a disc having radius a . Find centre of mass of remaing portion. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Figure shows a square plate of uniform thickness and side length √2m. One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
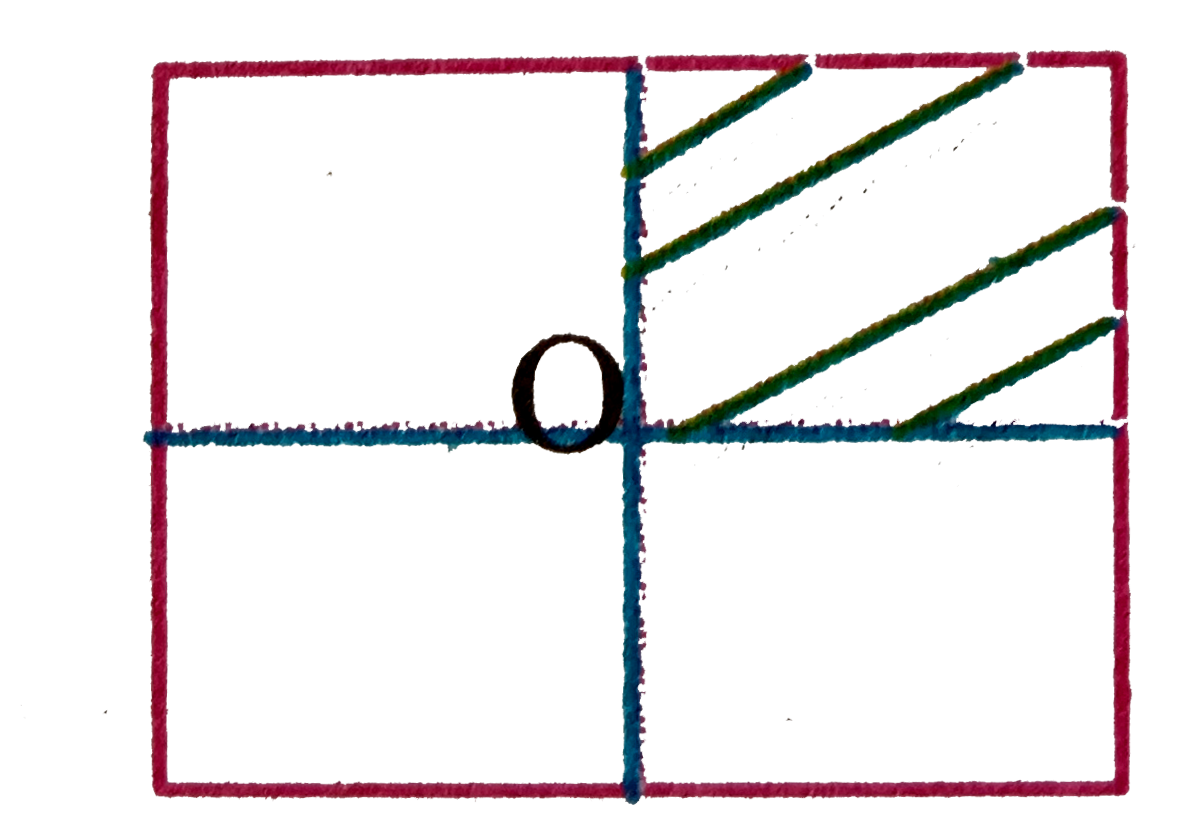 A1/3mB1/2mC1/6mD1/8m
A1/3mB1/2mC1/6mD1/8m - Question 2 - Select One
In the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
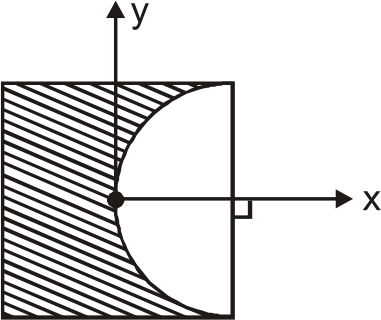 A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)
A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π) - Question 3 - Select One
From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
AR4π−2BR2πCRπ−2DR2π−2
Fron a sqaure plate of side a,a quarter circular disc of radius a is removed as shown in figure. Find the coordinates of centre of mass of the remaining part.
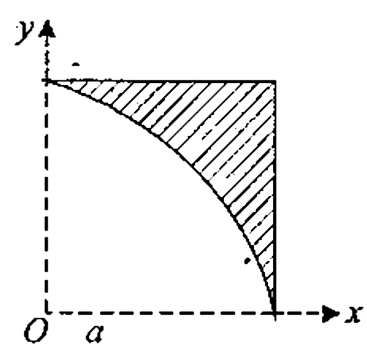 View Solution
View SolutionFind the centre of mass of the shaded portion of a disc.
 View Solution
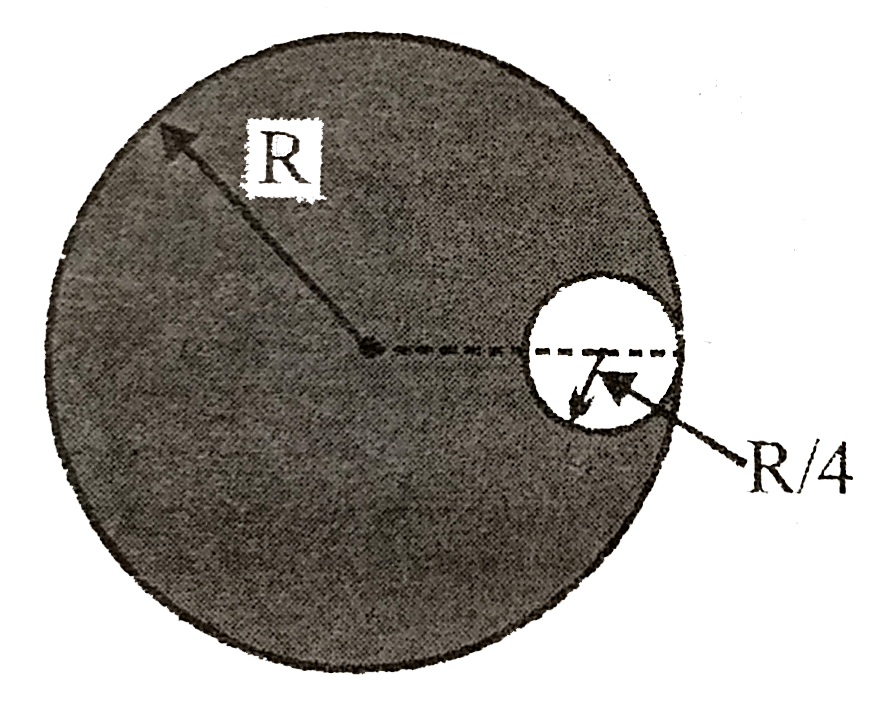
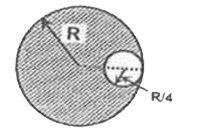
View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.
 View Solution
View SolutionA square shaped hole of side l=a2 is carved out at a distance d=a2 from the centre 'O' of a uniform circular disk of radius a. If the distance of the centre of mass of the remaining portion from O is −ax value of X (to the nearest integer) is _________.
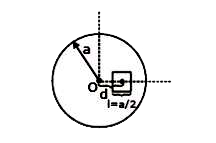 View Solution
View SolutionFrom a circle of radius a, an isosceles right angles triangle with the hypotenuse as the diameter of the circle is removed. The distance of the centre of mass of the remaining portion from the centre of the circle is
View Solution