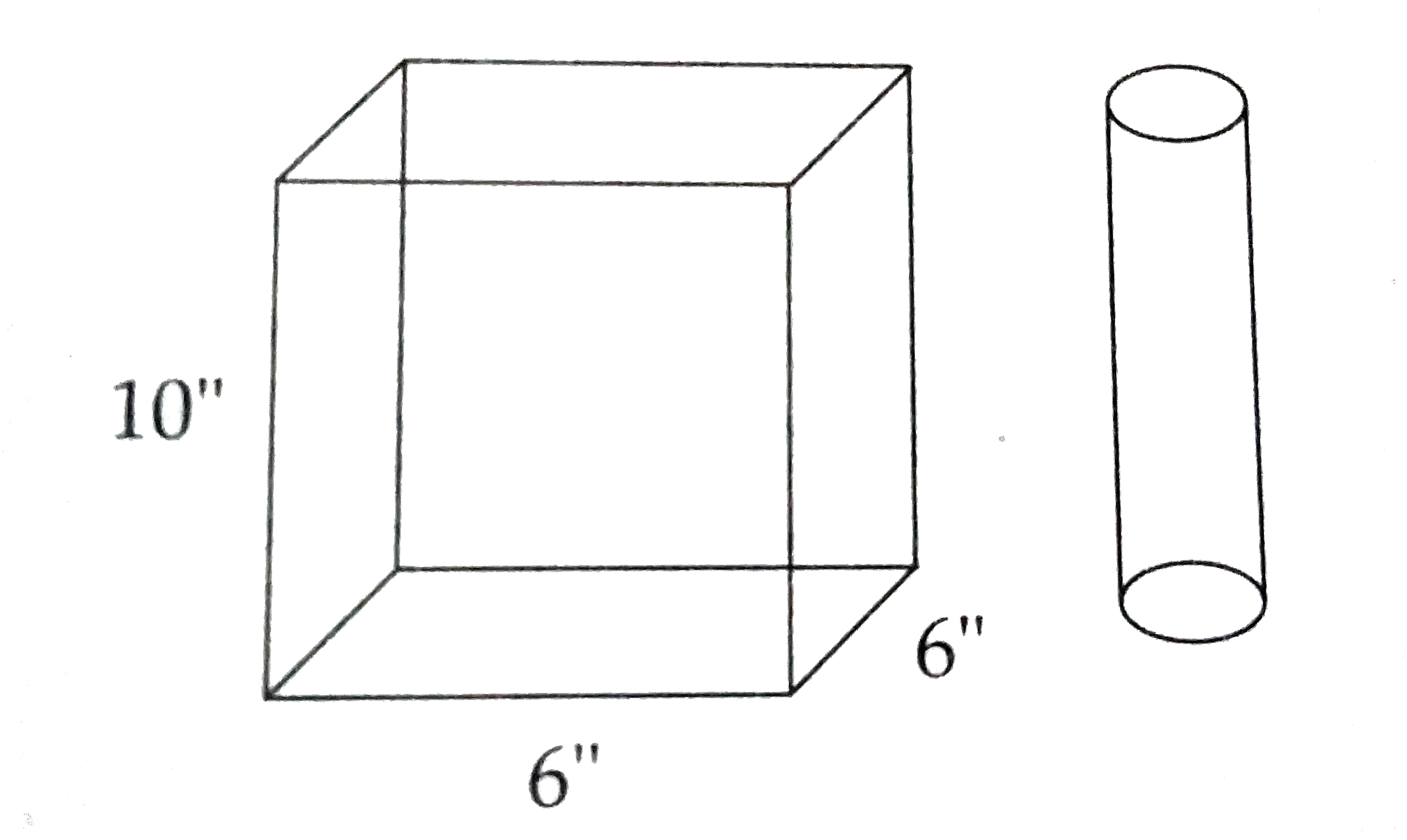
Figure shows a rectangular box and a cylinderical market, which has diameter 0.5'' and height 9''. If the box is filled with as many markers as possible, what percentage of the space will be unused ?
21.5%
24.6%
29.2%
31.8%
The correct Answer is:C
Since the markers are too long to be turned horizontal, they must be gathered together vertically. Put them in rows as long and wide as possible.
Since each marker has diamerter 0.5'', you can fit 12 across and 12 back, for a total of 144 markers. Now all that remains is to find the volume of the markers and the volume of the box.
The volume of the box =6×6×10=360
The volume of one marker =πr2h=π(0.25)2×9≈1.77.
The volume of all 144 markers ≈144×1.77≈254.88
The volume unsed is 360−254.88≈105.12
The percent unsed is 105.12360≈29.2%, so the answer is (C ).
You're covered the solid geomertry topics that you're likely to encounter on Math 2. You've reviewed the facts and formulas and learned some useful strategies. Now it's time for you to try another set of typical Math 2 solid geometry questions.
Topper's Solved these Questions
- BOOK - KAPLANCHAPTER - SOLID GEOMETRY EXERCISE - SOLID GEOMETRY FOLLOW - UP TEST5videos
SOLID GEOMETRY
- BOOK - KAPLANCHAPTER - SIMILARITY, CONGRUENCE, AND PROOFSEXERCISE - Multiple Choice Question10videos
SIMILARITY, CONGRUENCE, AND PROOFS
- BOOK - KAPLANCHAPTER - SYSTEM OF LINEAR EQUATION EXERCISE - Multiple Choice Question20videos
SYSTEM OF LINEAR EQUATION
Similar Questions
Two cylinders A and B are at rest in a box as shown in the figure. Cylinder A has a diameter of 3d and mass 120 kg. Cylinder B has a diameter of 2d and mass 36 kg . The width of the box is 4.5d. If all the contact surfaces are assumed to be smooth, then find the normal force exerted by the left wall on the cylinder B.
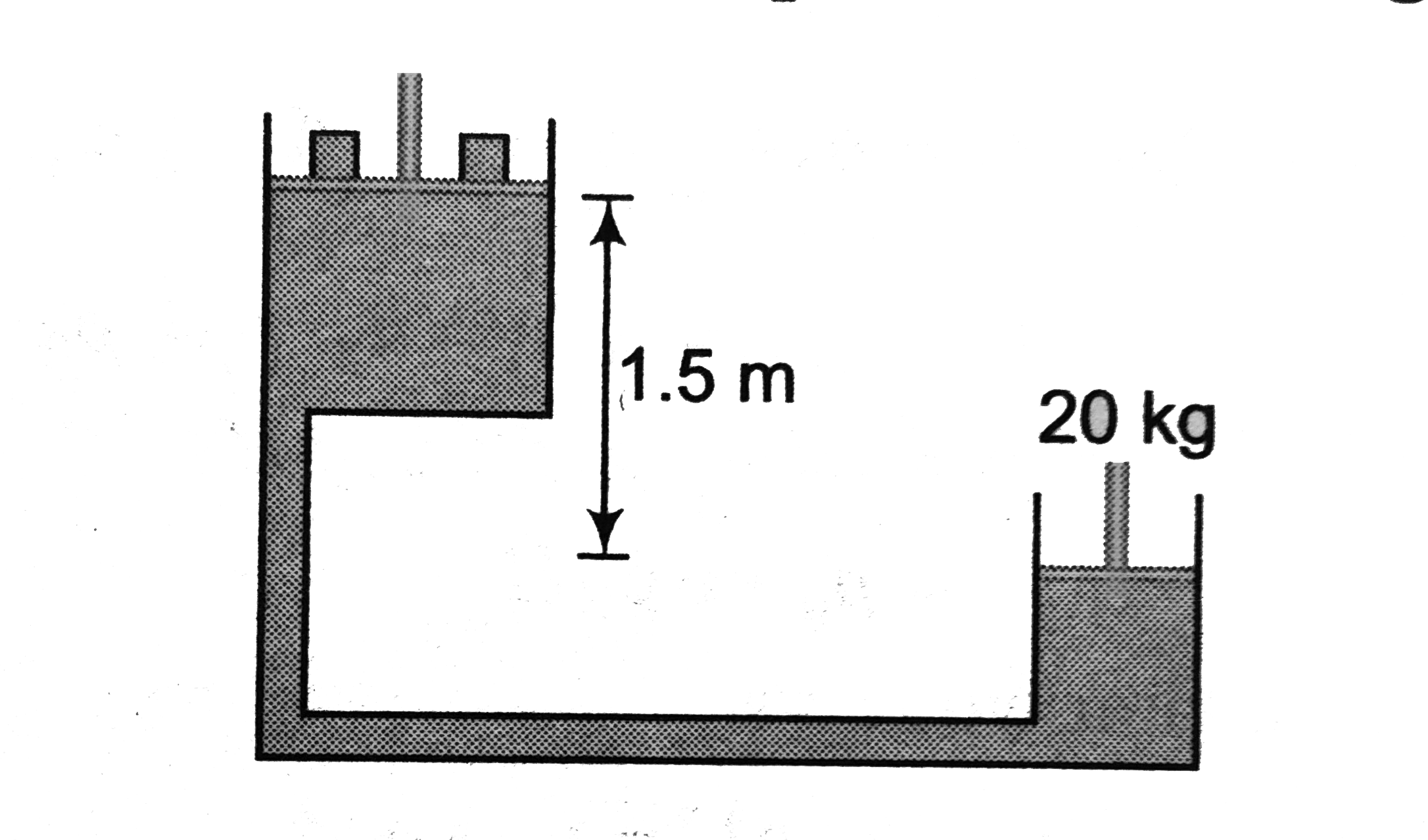
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
To ship figurines, the figurines are placed in a rectangular box and then small packing pellets are added. The base of the box has an area of 4.4∈2, and the height of the box is 6.5 in. IF the volume of the air in the box after the figures and pellets are added is 8.0∈3 , which of the following is closest to the combined volume of the figurines and pellets in the box?
A1.9∈3B20.6∈3C28.6∈3D117.84∈3 - Question 2 - Select One
A rectangular box with length 22 inches , width 5 inches , and height 5 inches is to be packed with steel balls of radius 2 inches in such a way that the centers of the balls are collinear. What is the maximum number of balls that can fit into the box, provided that no balls should protrude from the box ?
A0B5C6D10
Calculate the percentage error in the volume of a cylinder of diameter 2.4 cm and height 10.5 cm, both measured using a metre scale of least count 0.1 cm. What will be the percentage error if dimensions are measured using a vernier calipers of least count 0.01 cm?
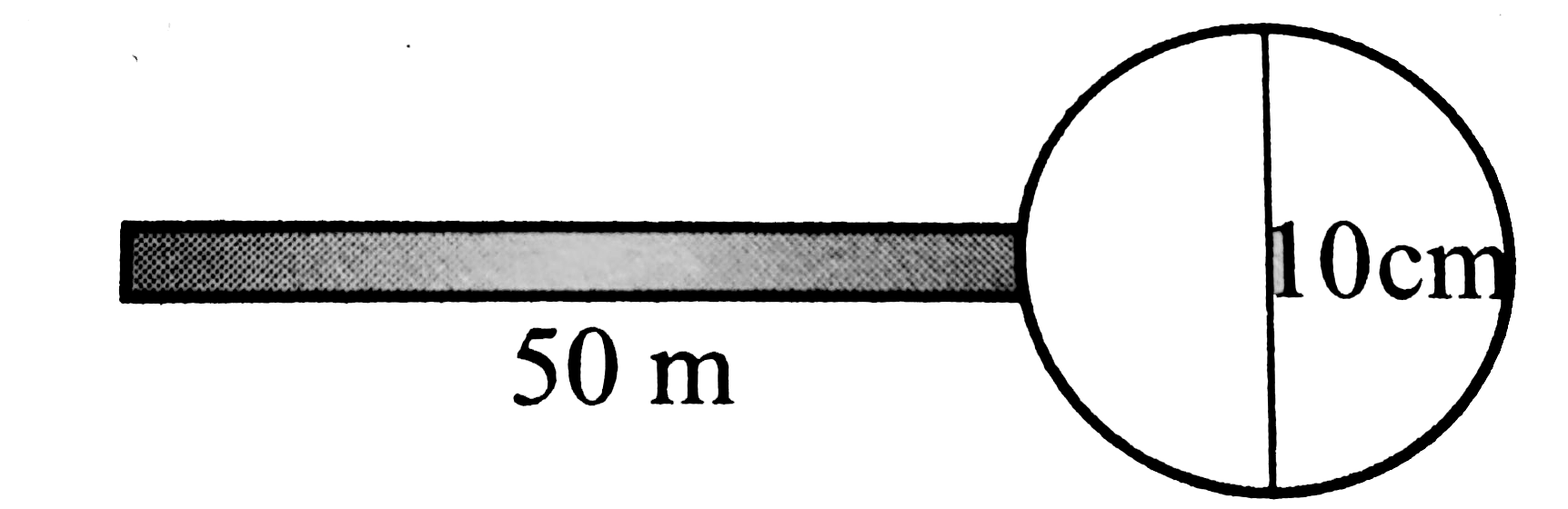
View SolutionFigure shows a thin uniform rod 50cm long and has a mass of 100g. A hollow metal ball is filled with air and has a diameter 10cm and total mass 50g is fixed to one end of the rod. At what point along its length will the ball and rod balance horizontally?
 View Solution
View Solution
In the figure above, a rectangular container with the dimensions 10 inches by 15 inches by 20 inches is to be filled with water, using a cylindrical cup whose radius is 2 inches and whose height is 5 inches. What is the maximum number of full cups of water that can be placed into the container without the water overflowing the container?View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height of the water in the long tube above the top when the water stops coming out of the hole.View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height h2 of the water in the long tube above top initially.View SolutionFigure shows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h0and pressure 2p0 where p0is the atmospheric pressure. There is a hole in the wall of tank at a depth h1below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.
 View Solution
View Solution

