
A block A of mass m is give a velocity v0 towards another block B of sae mass B. Is attached to an ideal spring of spring constant K. A makes a head on perfectly inelastic collision with B.
Answer the following two questions:
Q. Let the collision takes place at time t=0 choose the instant (s), when the spring is in its natural length.
π√2mK
2π√2mK
π√mK(√2+1)
2π√mK
The correct Answer is:A, C
Step by step video, text & image solution for A block A of mass m is give a velocity v_(0) towards another block B of sae mass B. Is attached to an ideal spring of spring constant K. A makes a head on perfectly inelastic collision with B. Answer the following two questions: Q. Let the collision takes place at time t=0 choose the instant (s), when the spring is in its natural length. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View Solution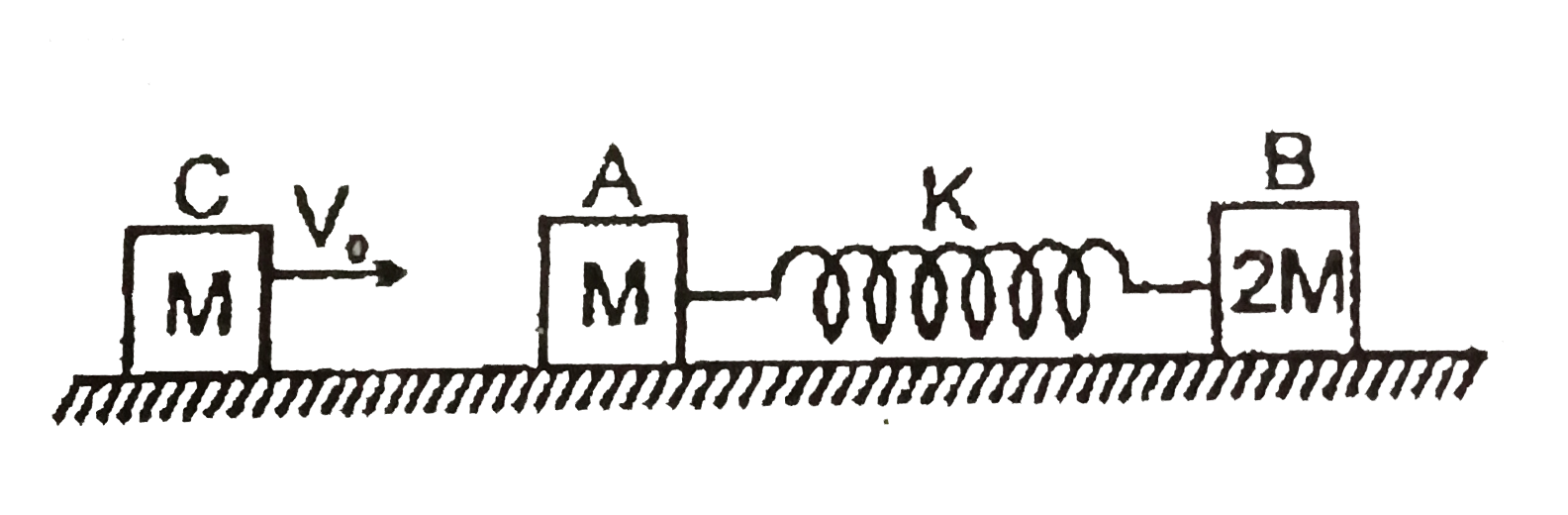 Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same
Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same
View Solution
Knowledge Check
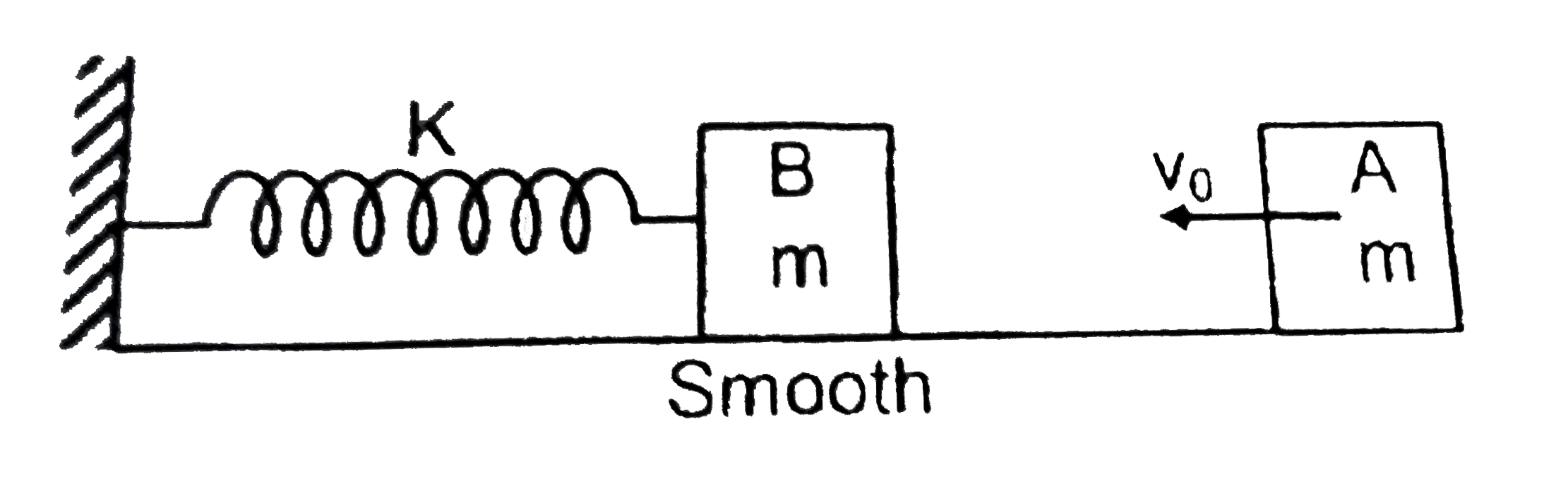
A block A of mass m is give a velocity v0 towards another block B of sae mass B. Is attached to an ideal spring of spring constant K. A makes a head on perfectly inelastic collision with B.
Answer the following two questions:
Q. Choose the correct option (s)AMaximum elongation in the spring during subsequent motion is 12√mv20KBMaximum elongation in the spring during subsequent motion is √mv202KCFinal velocity of block A is v02DFinal velocity of block A is V04A block of mass m moving with a velocity v0 collides with a stationary block of mass M to which a spring of stiffness k is attached, as shown in Fig. Choose the correct alternative(s)
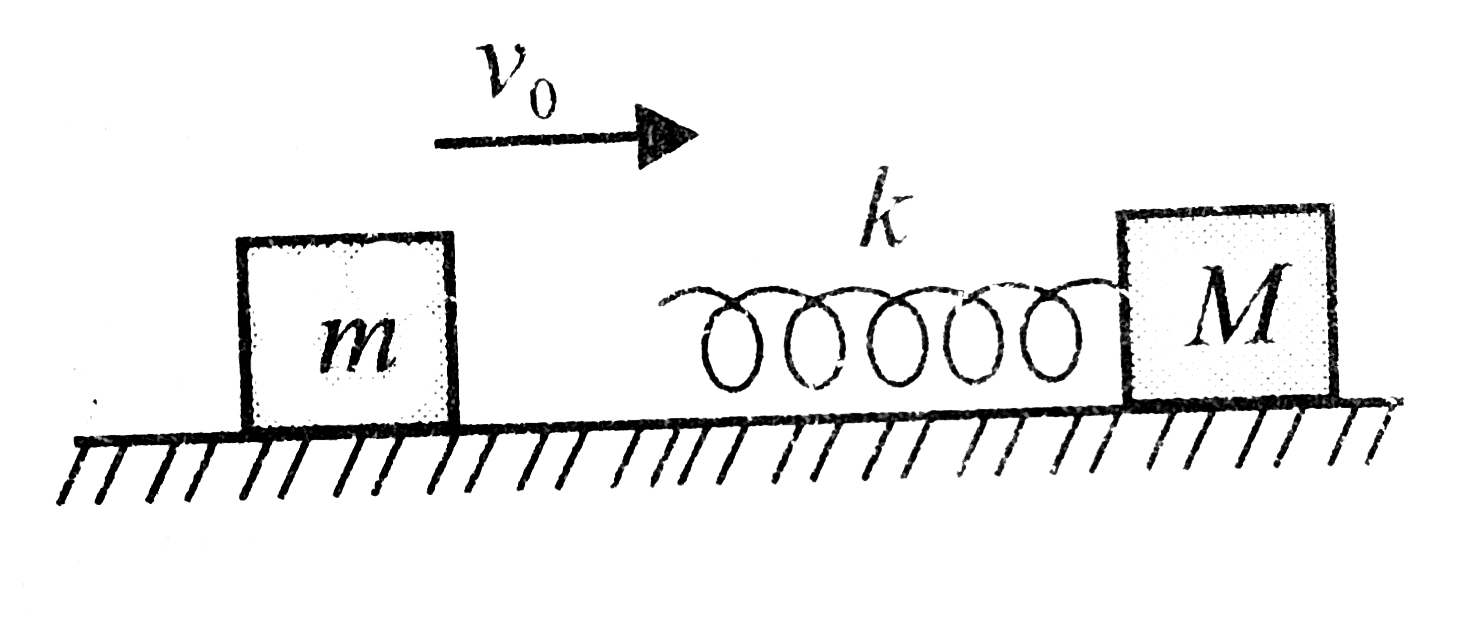 AThe velocity of the centre of mass is v0BThe initial kinetic energy of the system in the centre of mass frame is 14(mMM+m)v20CThe maximum compression in the spring is v0√(mMm+M1k)DWhen the spring is in the state of maximum compression, the kinetic energy in the centre of mass frame is zero
AThe velocity of the centre of mass is v0BThe initial kinetic energy of the system in the centre of mass frame is 14(mMM+m)v20CThe maximum compression in the spring is v0√(mMm+M1k)DWhen the spring is in the state of maximum compression, the kinetic energy in the centre of mass frame is zero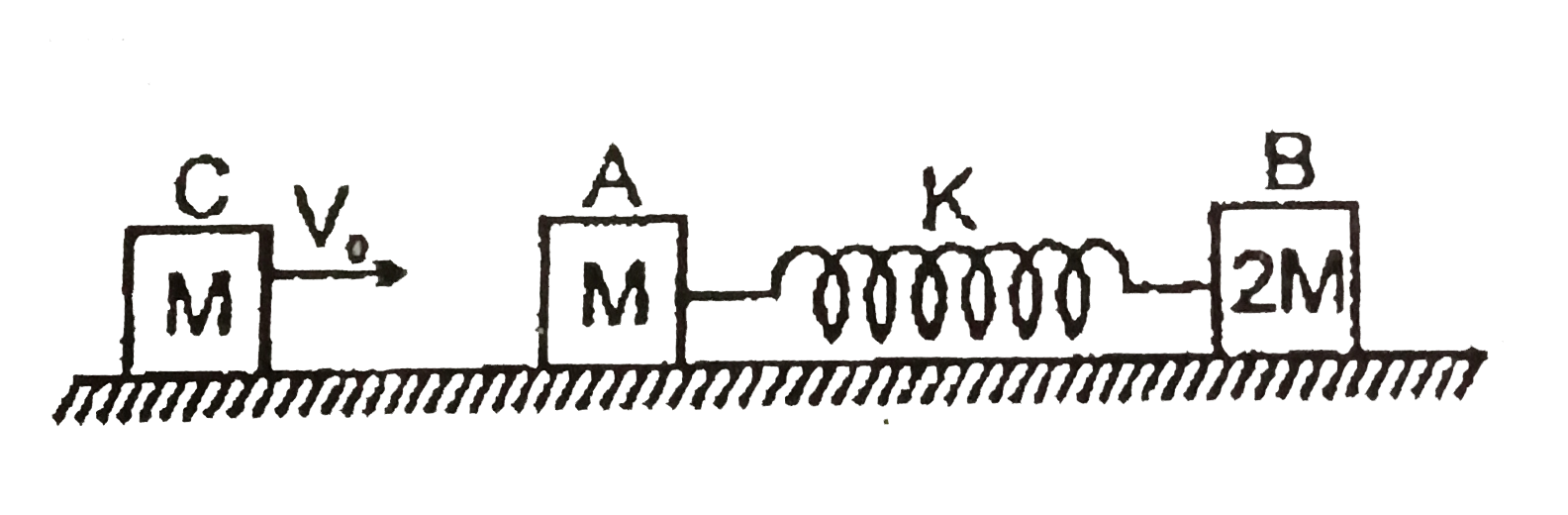 Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same A(MV20X20)B(MV202X20)C(3MV202X20)D(2MV203X20)
Block C of mass M is moving with velocity V0 and collides elastically with block A of mass M and connected to another block B of mass 2M through a spring of spring constant K. What is K if X0 is the compression of spring when velocity of A and B is same A(MV20X20)B(MV202X20)C(3MV202X20)D(2MV203X20)
Block of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.

View Solution
