
In shown figure a triangular wedge and a cylinder each having equal mass m are released from rest. The vertical wall and horizontal surface are frictionless and between the wedge and the cylinder friction is sufficient to allow cylinder to roll over it choose correct option(s)
Acceleration of wedge is
Minimum value of coefficient of friction between wedge and cylinder without slipping is
minimum value of coefficient of friction between wedge an cylinder for rolling without slipping is
if , the contact force between cylinder and wedge is 100 N.
The correct Answer is:A, B, D

.(1)
..(2)
.(3)
for rolling
.(4)
contact force
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
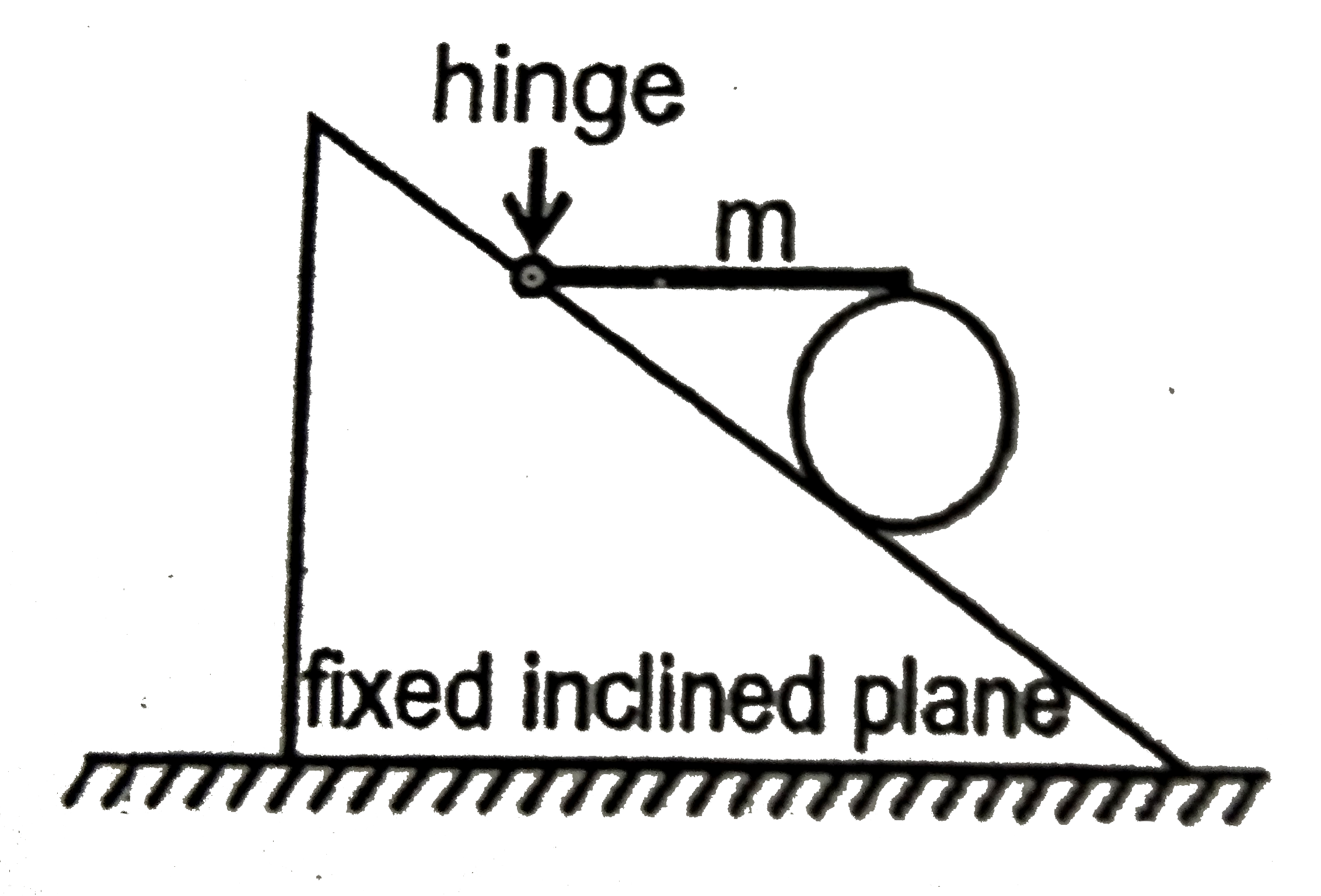
A horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :
View SolutionA uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

View Solution
Knowledge Check
A horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.

The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :A1:1B2:√3C2:1D√2:1A uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is
 AMsinθ1−sinθBMcosθ1+sinθCMsinθ1+sinθDMcosθ1−cosθ
AMsinθ1−sinθBMcosθ1+sinθCMsinθ1+sinθDMcosθ1−cosθA solid cylinder of mass m rolls without slipping down an inclined plane making an angle θ with the horizontal. The frictional force between the cylinder and the incline is
AmgsinθBmgsinθ3CmgcosθD2mgsinθ3
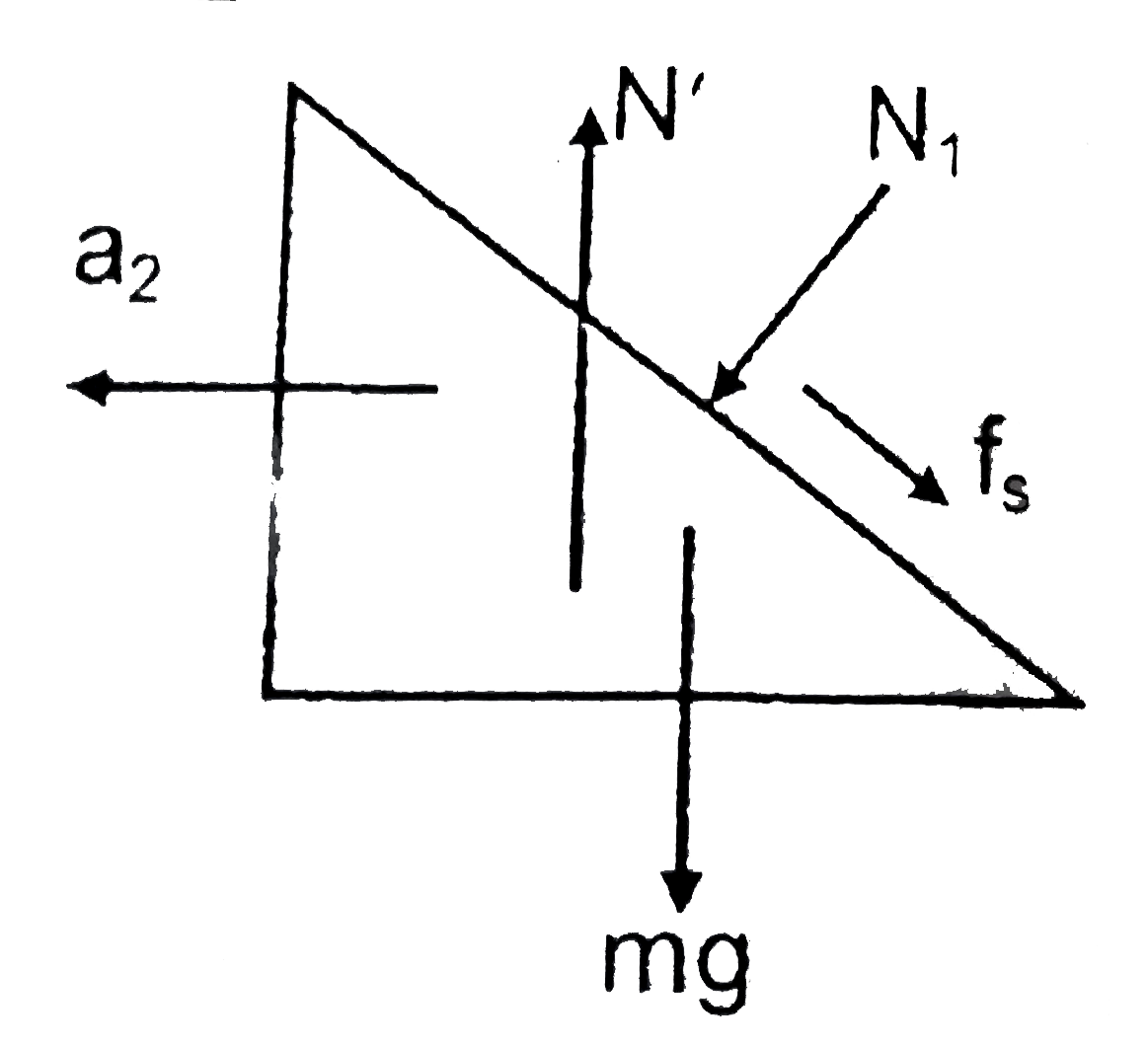
A block of mass m is at rest on wedge as shown in figure. Let N be the normal reaction between two and f the force of friction, then choose the wrong option.
View SolutionIn the arrangement shown in figure the masses of the wedge M and the body m are known. The appreciable friction exists only between the wedge and the body m, the friction coefficient being equal to k. The masses of the pulley and the thread are negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.

View SolutionIn the arrangement shown in figure the masses of the wedge M and the body m are known. The appreciable friction exists only between the wedge and the body m, the friction coefficient being equal to k. The masses of the pulley and the thread are negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.

View SolutionA block of mass m is at rest on wedge as shown in figure. Let N be the normal reaction between two and f the force of friction, then choose the wrong option.

View SolutionThere is sufficient friction between long plank of mass 2m and cylinder of mass m and radius R to prevent slipping. Whole system is placed on the smooth inclined surface. Now, force F=3mgsinθ is applied on the ideal string wrapped over the cylinder as shown in figure. Choose correct option:

View Solution
