A rod of lengths L is supported two ideal strings of length l such that the system hangs in a vertical plane.
Case 1: Rod is kept horizontal displaced slightly perpendicular to the plane and allowed by oscillate.
Case 2: Rod is given a small twist about central axis and then allowed to oscillate.
Let T1,T2 be the period of oscillations in the two respective cases.

T1=2π√lg
T1=2π√l2g
T2=2π√l6g
T2=2π√l3g
The correct Answer is:A, D
Let θ be the angle that the rod rotates about its its central axis and ϕ be the angle made by string with the vertical.
−(2Tϕ)L2=mL212d2θdt2
⇒d2θdt2=−(6gL)ϕ
or d2θdt2=−(3gl)θ
⇒T2=2π√l3g

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
View SolutionA rod of length l and mass m is capable of rotating freely about an axis passing through a hole at the end. The period of oscillation of this physical pendulum is
View Solution
Knowledge Check
A thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
A2π√lgB2π√2l3gC2π√3l2gD2π√l3gA thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
A12mB34mC1 mD23mA man is swinging on a swing made of 2 ropes of equal length L and in direction perpendicular to the plane of paper. The time period of the small oscillations about the mean position is
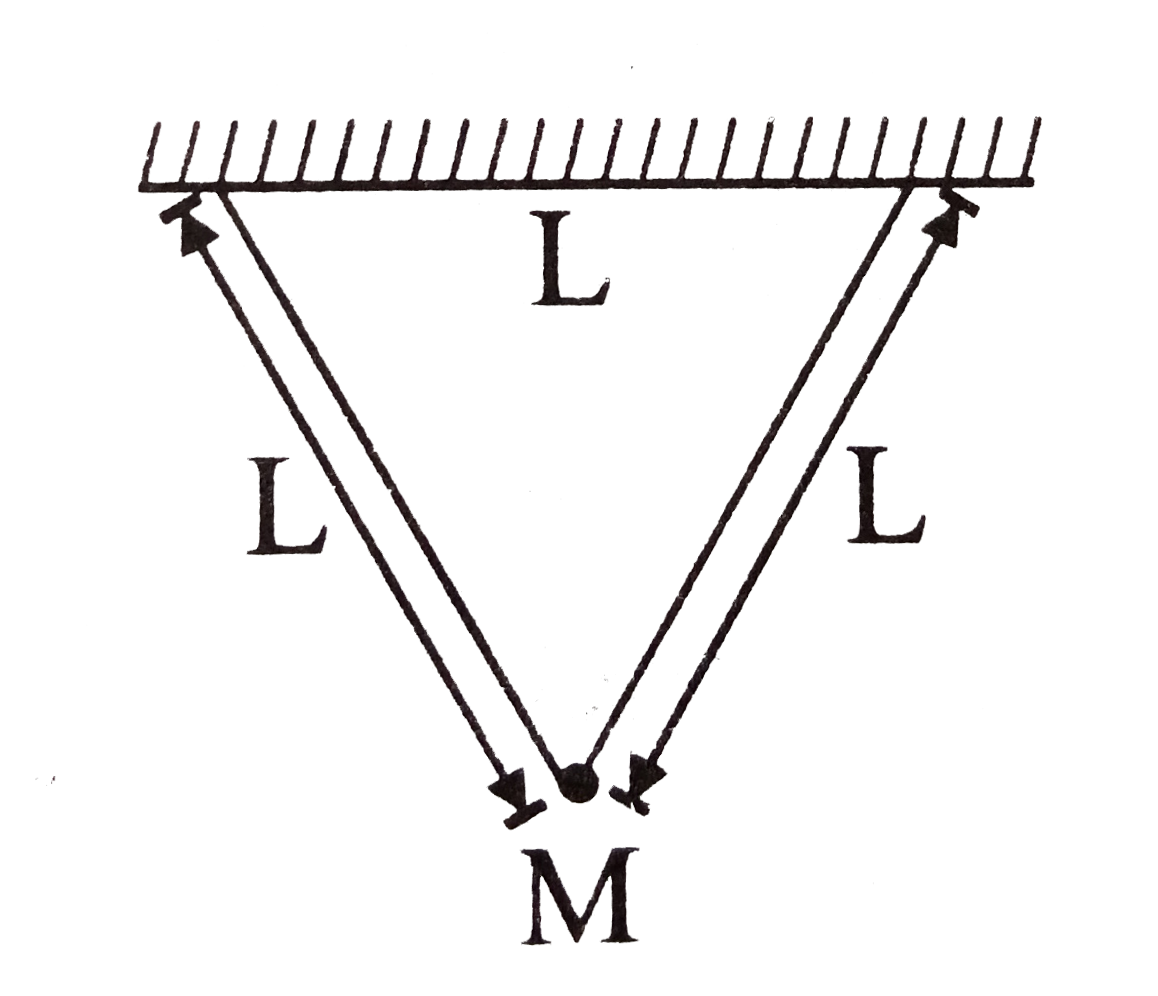 A2π√L2gB2π√√3L2gC2π√L2√3gDπ√Lg
A2π√L2gB2π√√3L2gC2π√L2√3gDπ√Lg
Two identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View Solution
