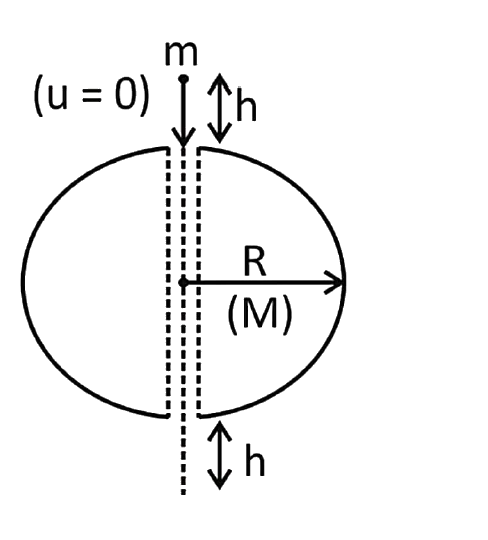
A small particle is dropped from a height R in front of a narow tunnel dug inside the earth (along a diameter). Let M be the mass of earth, R be radius of earrth. Let v0,T be speed of particle when it reaches A and time taken by particle to go from A to B respectively. Assuming mass of particle to be negligible as compare to mass of earth, pick the correct option(s)

V0=√GM2R
V0=√GMR
R=π2√R3GM
T=π√R3GM
The correct Answer is:B, C
−GMm2R=−GMmR+12mv20
⇒v0=√GMR
while in the tunnel,
d2xdt2=−(GMR3)x
v20=GMR=ω2(a2−R2)⇒a=√2R
⇒TA→B=14×2π√R3GM

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A particle of mass m is dropped from a great height h above the hole in the earth dug along its diameter.
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
View Solution
Knowledge Check
A particle of mass m is dropped from a great height h above the hole in the earth dug along its diameter.
AThe motion of the particle is simple harmonicBThe motion of the particle is periodicCThe speed of the particle at the centre of earth equals √2GM(R+h) , where R and M are the radius and mass of the earth respectivelyDThe speed of the particle at the centre of earth equals √GM(R+3h)R(R+h), where R and M are the radius and mass of the earth respectivelyA ball of mass m is dropped from a height h equal to the radius of the earth above the tunnel dug through the earth as shows in the figure. Choose the correct options. (Mass of earth =M)
 AParticle will oscillate through the earth to a height h on both sidesBParticle will execute simple harmonic motionCMotion of the particle is periodicDParticle passes the centre of earth with a sped υ=√2GMR
AParticle will oscillate through the earth to a height h on both sidesBParticle will execute simple harmonic motionCMotion of the particle is periodicDParticle passes the centre of earth with a sped υ=√2GMRIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle isA√2GMRB√GMRC√3GM2RD√GM2R
A ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is

View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View SolutionA ball of mass m is dropped from a height h equal to the radius of the earth above the tunnel dug through the earth as shows in the figure. Choose the correct options. (Mass of earth =M)

View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle is
View Solution
